Courbes mathématiques avec Latex
Dessiner des courbes avec LaTeX
Même si l'intérêt global de
est loin de résider uniquement dans la rédaction de textes scientifiques contenant de belles formules mathématiques, cela en reste néanmoins un de ses atouts.
Tracer des courbes en tout genre (courbe définie par son expression
.png)
,
courbe paramétrique, en coordonnées polaires, ...) est donc la moindre des choses.
Courbe représentative d'une fonction
Tracer la courbe représentative d'une fonction définie par son expression
est donc des plus naturels.
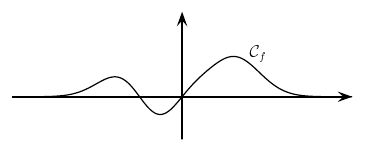
Par exemple, soit la fonction
définie par l'expression
.Sa représentation graphique peut se dessiner de la façon suivante, en utilisant
psplot
(dans un environnement pspicture ou non):
- Code:
\psset{unit=1cm,arrowsize=7pt}
\begin{pspicture}(-5,-1.5)(5,2.5)
\psline[linewidth=1.3pt]{->}(-4,0)(4,0)
\psline[linewidth=1.3pt]{->}(0,-1)(0,2)
\psplot[plotpoints=1000]%
{-4}{4}{ x 4 exp x add 2.718 -1 x 2 exp mul 0.2 add exp mul}
\rput(1.8,1.){$\mathcal{C}_f$}
\end{pspicture}
- Affichage:
-
psplot se fait en notation polonaise inversée, voir là par exemple.
L'expression peut aussi être donnée en notation algébrique "naturel" en incluant l'option "algebraic":
\psset{unit=1 cm, algebraic=true}.
Représentation des lois binomiale et normale
Les lois normales et binomiales sont fournies prêtes à l'emploi dans le package
ps-func, à charger donc dans le préambule par \usepackage{pst-func}
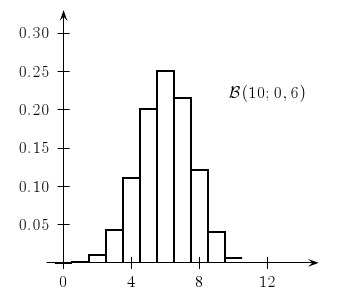
Pour la loi binomiale:
- Code:
\psset{xunit=0.4cm,yunit=18cm,arrowsize=5pt}
\begin{pspicture}(-4,-0.03)(25,0.34)
\rput(12,0.22){$\mathcal{B}(10;0,6)$}
\psaxes[Dx=4,Dy=0.05,dy=0.05\psyunit]{->}(0,0)(-1,0)(15,0.33)
\psBinomial[linewidth=1.2pt]{10}{0.6}
\end{pspicture}
- Affichage:
-
- Code:
\psset{xunit=0.35cm,yunit=20cm,arrowsize=5pt}
\begin{pspicture}(-7,-0.03)(25,0.15)
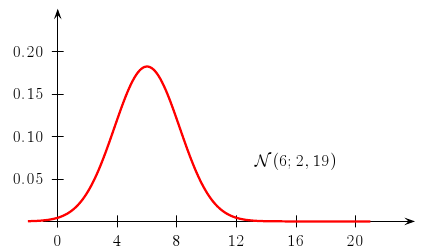
\rput(16,0.07){$\mathcal{N}(6;2,19)$}
\psaxes[Dx=4,Dy=0.05,dy=0.05\psyunit]{->}(0,0)(-1,0)(24,0.25)
\psGauss[linecolor=red,linewidth=1.5pt,mue=6,sigma=2.19]{-2}{21}
\end{pspicture}
- Affichage:
-
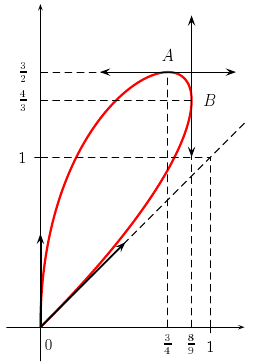
Courbes planes paramétrées
Les courbes planes paramétrées se tracent, non pas via
psplot, mais via parametricplot, par exemple, pour la courbe paramétrée définie par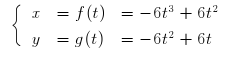 
(ici aussi la notation polonaise inversée est utilisée, par défaut, mais on pourrait là aussi tout aussi bien utiliser l'option
algebraic=true dans psset)
- Code:
\psset{xunit=4cm,yunit=4cm}
\begin{pspicture}(-0.3,-0.1)(2,1.75)
\psaxes{->}(0,0)(-.2,-.2)(1.2,1.9)
\rput(0.05,-0.1){$0$}
\parametricplot[plotpoints=200,linecolor=red,linewidth=1.5pt]{0}{1}{
-6 t 3 exp mul 6 t 2 exp mul add
-6 t 2 exp mul 6 t mul add
}
% Point 0
\psline[linewidth=1.2pt,arrowsize=5pt]{->}(0,0)(0,0.55)
\psline[linewidth=1.2pt,arrowsize=5pt]{->}(0,0)(0.5,0.5)
\psline[linestyle=dashed](0,0)(1.2,1.2)
\psline[linestyle=dashed](1,0)(1,1)(0,1)
% Point A
\psline[linestyle=dashed](0.75,0)(0.75,1.5)(0,1.5)
\rput(0.75,-0.1){$\frac{3}{4}$}\rput(-0.1,1.5){$\frac{3}{2}$}
\psline[arrowsize=5pt]{<->}(0.35,1.5)(1.15,1.5)
\rput(0.75,1.6){$A$}
% Point B
\psline[linestyle=dashed](0.8888,0)(0.8888,1.3333)(0,1.3333)
\rput(0.8888,-0.1){$\frac{8}{9}$}\rput(-0.1,1.3333){$\frac{4}{3}$}
\psline[arrowsize=5pt]{<->}(0.8888,1.)(0.8888,1.8333)
\rput(1.,1.3333){$B$}
\end{pspicture}
- Affichage:
-
