Approximation numérique d'integrales
Éléments de correction
du cours 
Exercice 1:
Soit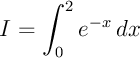
- On a
![\[\bgar{ll}I&=\Bigl[-e^{-x}\Bigr]_0^2\\[.8em]
&=-e^{-2}-\lp-e^0\rp\\[.8em]&=1-e^{-2}\simeq0,865\enar\]](fich-IMG/2.png)
- L'approximation par la méthode des rectangles à gauche s'écrit
![\[I=\int_a^b f(x)dx\simeq h\sum_{i=0}^{n-1}f\lp x_i\rp\]](fich-IMG/3.png)
où la suite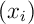 est une discrétisation de l'intervalle
est une discrétisation de l'intervalle ![$[0;2]$](fich-IMG/5.png) d'intégration:
d'intégration:
![\[\newcommand{\addu}[1]{#1 1 add}
\begin{pspicture}(-2,-1.7)(11,1)
\psline[arrowsize=8pt,linewidth=1.4pt]{->}(-.5,0)(10,0)
\multido{\i=0+1}{3}{\psline(\i,-.2)(\i,.2)}
\multido{\i=0+1}{2}{\psline[arrowsize=6pt]{<->}(\i,-1)(!\addu{\i}\space-1)}
\rput(.5,-1.3){$h$}\rput(1.5,-1.3){$h$}
\rput(2.8,-1){$\dots$}
\rput(0,.4){$a\!=\!0$}
\rput[r](0.2,-.4){$x_0$}
\rput(1,-.4){$x_1$}
\rput(2,-.4){$x_2$}
\rput(4,-.4){$\dots$}
\psline(4.8,-.2)(4.8,.2)\rput(4.8,-.4){$x_i$}
\rput(5.5,-.4){$\dots$}
\psline(8,-.2)(8,.2)\rput(8,-.4){$x_{n-1}$}
\rput(8.8,.4){$b\!=\!2$}\psline(8.8,-.2)(8.8,.2)\rput[l](8.8,-.4){$x_n$}
\psline[arrowsize=6pt]{<->}(8,-1)(8.8,-1)\rput(8.5,-1.3){$h$}
\end{pspicture}\]](fich-IMG/6.png)
Avec un pas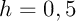 , on a
, on a 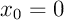 ,
, 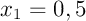 ,
, 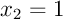 ,
, 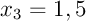 et
et 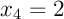 ,
et alors
,
et alors
![\[I\simeq0,5\Bigl(f(0)+f(0,5)+f(1)+f(1,5) \Bigr)\simeq1,099\]](fich-IMG/13.png)
- Avec un pas
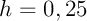 ,
,
![\[I\simeq0,25\Bigl(f(0,25)+f(0,5)+f(0,75)+\dots f(1,75) \Bigr)\simeq0,977\]](fich-IMG/15.png)
- Pour commenter, on calcule l'erreur relative:
- avec un pas
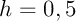 ,
,
![\[\varepsilon_r\simeq\left|\dfrac{0,865-1,099}{0,865}\right|\simeq0,27\]](fich-IMG/17.png)
et avec un pas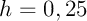 ,
,
![\[\varepsilon_r\simeq\left|\dfrac{0,865-0,977}{0,865}\right|\simeq0,13\]](fich-IMG/19.png)
Bien sûr les calculs avec des valeurs plus petites du pas nécessitent une automatisation des calculs, ou programmation: c'est l'objectif en TP.
- avec un pas
Exercice 2:
On reprend l'intégrale
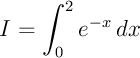
- L'approximation par la méthode des trapèzes s'écrit
![\[\int_a^b f(x)dx\simeq\dfrac{h}{2}\lp f\lp x_0\rp+\dsp2\sum_{i=1}^{n-1}f\lp x_{i}\rp+f\lp x_n\rp\rp\]](fich-IMG/21.png)
et donc,- avec un pas
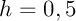 , la discrétisation de l'intervalle est la même qu'à l'exercice précédent, et alors
, la discrétisation de l'intervalle est la même qu'à l'exercice précédent, et alors
![\[\bgar{ll}I&\simeq\dfrac{0,5}2\Biggl(
f(0)+2\Bigl(f(0,5)+f(1)+f(1,5)\Bigr) + f(2)\Biggr)\\[1.3em]
&\simeq0,8826\enar\]](fich-IMG/23.png)
- avec un pas
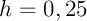 , on a
, on a
![\[\bgar{ll}I&\simeq\dfrac{0,25}2\Biggl(
f(0)+2\Bigl(f(0,25)+f(0,5)+\dots+f(1,75)\Bigr) + f(2)\Biggr)\\[1.3em]
&\simeq0,8692\enar\]](fich-IMG/25.png)
- avec un pas
- Pour commenter, on calcule l'erreur relative:
- avec un pas
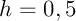 ,
,
![\[\varepsilon_r\simeq\left|\dfrac{0,8647-0,8826}{0,8647}\right|\simeq2.10^{-2}\]](fich-IMG/27.png)
et avec un pas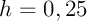 ,
,
![\[\varepsilon_r\simeq\left|\dfrac{0,8647-0,8692}{0,8647}\right|\simeq5.10^{-3}\]](fich-IMG/29.png)
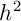 .
.
- avec un pas
Exercice 3:
On reprend à nouveau l'intégrale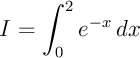
- Avec un pas
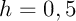 , donc toujours la discrétisation
, donc toujours la discrétisation 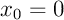 ,
, 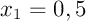 ,
, 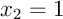 ,
, 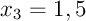 et
et 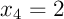 , l'approximation de l'intégrale par la méthode de Simpson s'écrit,
, l'approximation de l'intégrale par la méthode de Simpson s'écrit,
soit![\[I\simeq
=\dfrac{h}{6}\sum_{i=0}^{n-1}\lb
f\lp x_i\rp+4f\lp\dfrac{x_i+x_{i+1}}{2}\rp + f\lp x_{i+1}\rp
\rb\]](fich-IMG/38.png)
![\[\bgar{lll}I&\simeq
\dfrac{0,5}6\Bigl[
&f(0)+4f\lp0,25\rp + f(0,5)\\[.6em]
&&f(0,5)+4f(0,75)+f(1)\\[.6em]
&&f(1)+4f(1,25)+f(1,5)\\[.4em]
&&f(1,5)+4f(1,75)+f(2)
\ \Bigr]\\
&\simeq0,86468
\enar
\]](fich-IMG/39.png)
- L'erreur relative pour cette méthode est
![\[\varepsilon_r\simeq2.10^{-5}\]](fich-IMG/40.png)
ce qui est, avec le même pas, 10 000 fois plus précis que la méthode des rectangles, et 1000 fois plus précis que la méthode des trapèzes.
Voir aussi:
- Modélisation, simulation et résolution numérique de problème
- Introduction: modélisation, simulation et approximation numérique d'un problème
- Partie III: approximation numérique de dérivées
- Partie III: approximation numérique de dérivées
- Partie IV: Intégration numérique: calcul approché d'intégrales