Fabrication de pièces dans deux ateliers

Dans une entreprise deux ateliers fabriquent les mêmes pièces. L'atelier 1 fabrique en une journée deux fois plus de pièces que l'atelier 2. Le pourcentage de pièces défectueuses est 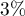$3\%$ pour l'atelier 1 et 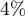$4\%$ pour l'atelier 2. On prèlève une pièce au hasard dans l'ensemble de la production d'une journée.

Déterminer la probabilité que cette pièce provienne de l'atelier 1.
Déterminer la probabilité que cette pièce provienne de l'atelier 1 sachant qu'elle est défectueuse.

Correction

D'après l'énoncé, les 2/3 des pièces produites proviennent de l'atelier 1, c'est-à-dire que .
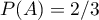On a

$P(A\cap D)=P_A(D)P(A)=0,03\tm\dfrac23=\dfrac1{50}$

et de même

$P(B\cap D)=0,04\tm\dfrac13=\dfrac1{75}$

et donc que

$P(D)=P(A\cap D)+P(B\cap D)=\dfrac1{30}$

et ainsi, on a

$P_D(A)=\dfrac{P(A\cap D)}{P(D)}=\dfrac35$

Cacher la correction

Tag:Probabilités conditionnelles - indépendance

Autres sujets au hasard: