next up previous
suivant: Numérisation d'un signal

Prêts gigognes ou emboîtés/étagés

Lissage de mensualités

Y. Morel


Prérequis: avant de s'attaquer aux développements de cette page sur les prêts gigognes, et comme il s'agit d'emboîtements de prêts à taux d'intérêts, il peut être important (essentiel ?) de connaître le fonctionnement d'un prêt simple à taux d'intérêts fixe sur une durée donnée. Ces détails se trouvent là Lien

Généralement plus un prêt est court moins il est coûteux, le taux d'intérêts pratiqué est plus bas et de plus l'assurance de celui-ci est aussi moins onéreuse (une durée plus brève va de pair avec un risque moindre…).
Malheureusement, plus un prêt est sur une courte durée, plus les mensualités sont logiquement élevées. Ainsi, la durée pour un prêt s'impose en pratique assez d'elle même, fonction directe de la capacité de remboursement de l'emprunteur.

Néanmoins, il est possible en théorie d'utiliser le principe précédent pour diminuer le coût global d'un emprunt. Il faux donc pour cela diminuer le montant de l'emprunt !
Le principe est alors de scinder l'emprunt global en (au moins) deux autres emprunts, et d'en considérer (au moins) un sur une durée plus courte.
L'opération de lissage consiste alors à calculer les mensualités de telle sorte que celles-ci soit constantes tout au long de la durée totale du prêt, pendant une première phase avec les deux prêts superposés, ou emboîtés, et pendant la deuxième ou ensuite il ne reste plus que le prêt plus long.

Ce principe général est aussi celui du rachat de crédits: étant redevable de plusieurs crédits, certains organismes (banques, courtiers, usuriers …) propose de "rassembler" tous ceux-ci en un seul, avec un "taux global plus avantageux" …

Cas de deux prêts

Principe de l'emboîtage et du lissage de 2 prêts


On cherche à emprunter un montant global $E$ que l'on découpe en deux sous-emprunts qui s'emboîtent en s'étalant sur des durées différentes: un emprunt plus court d'un montant $E_c$, sur une durée $N_c$ et à un taux d'intérêt $t_c$, et l'autre d'un montant $E_l$ sur une durée plus longue $N_l$ à un taux d'intérêt $t_l$.
On a bien sûr bien sûr globalement $E=E_c+E_l$.

On distingue deux phases de remboursement successives, voir aussi le graphique ci-dessous et/ou l'outil de calcul en ligne
  • Première période: de 0 à 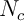$N_c$ mois.
    Le prêt court est remboursé sur cette période comme un prêt simple à taux fixe, voir la partie précédente. On notera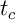 $t_c$ son taux d'intérêt mensuel, et on a donc le montant 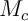$M_c$ des mensualités versées pour rembourser ce prêt:
    \[M_c=\dfrac{E_ct_c}{1-(1+t_c)^{-N_c}}\]


    Pendant cette première période, on rembourse aussi chaque mois une partie du second prêt. On notera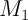 $M_1$ les mensualités correspondantes.
    Ainsi, durant cette première période le montant total des mensualités est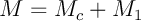 $M=M_c+M_1$.
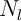  • Deuxième période: de $N_c$ à $N_l$ mois
    Après $N_c$ mois, le premier emprunt est totalement remboursé, donc clos, et il ne reste plus que le résidu du premier, partie non encore remboursée, au taux $t_l$.
    On notera $M_2$ les mensualités dans cette deuxième période.

    On parle de lissage, ou de mensualités lissées, lorsque les mensualités sont identiques sur toute la durée de l'emprunt global, c'est-à-dire pendant la première période et la deuxième période, ou encore en termes algébriques

    \[M=M_c+M_1=M_2\]

Ce cadre étant posée, la première question est: quel lien y-a-t'il entre toutes ces grandeurs: $E_c$, $t_c$, $M_c$ du prêt court, et $E_l$, $t_l$, $M_1$ et $M_2$ du prêt long ?

\[\psset{unit=1cm,arrowsize=7pt} \begin{pspicture}(-1.2,-1.2)(10.4,5.7) \psline{->}(-.2,0)(10,0) \psline{->}(0,-.2)(0,5.4) \pspolygon[fillstyle=solid,fillcolor=blue](0,0)(9,0)(9,4.5)(0,4.5) \pspolygon[fillstyle=solid,fillcolor=magenta](0,0)(6,0)(6,3)(0,3) % \rput(0,-.5){0} \psline(6,0)(6,-.2)\rput(6,-.5){$N_c$} \psline(9,0)(9,-.2)\rput(9,-.5){$N_l$} %\psline(-.2,3)(0,3)\rput[r](-.3,3){$M_c$} \psline{->}(-.35,0)(-.35,3)\rput[r](-.5,1.5){$M_c$} \psline{->}(-.35,3.02)(-.35,4.5)\rput[r](-.5,3.75){$M_1$} \psline(-.2,4.5)(0,4.5) \psline{->}(9.35,.05)(9.35,4.5)\rput[l](9.45,2.5){$M_2$} \psline{->}(6,-.9)(9,-.9)\rput(7.5,-1.3){$N_R=N_l-N_c$} \end{pspicture}\]


Calcul des mensualités
Les mensualités pour le prêt court sont, comme détaillé là Lien,
\[M_c=\dfrac{E_ct_c}{1-(1+t_c)^{-N_c}}\]


Concernant le prêt long, la première question est de savoir, en versant des mensualités $M_1$, quelle sera la part de capital remboursée pendant la première phase d'une durée $N_c$.

On reprend pour cela le raisonnement et les calculs de la partie précédente.

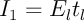  • $1^\text{er}$ mois: le montant des intérêts versés est $I_1=E_lt_l$, la partie de capital remboursée est 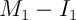$M_1-I_1$, et donc le capital restant à rembourser après le premier mois est
    \[\bgar{ll} C_1&=E_l-(M_1-I_1)\\[.6em] &=E_l-M_1+I_1\\[.6em] &=E_l-M_1+E_lt_l\\[.6em] &=E_l(1+t_l)-M_1 \enar\]


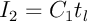  • $2^\text{ème}$ mois: le montant des intérêts versés est maintenant $I_2=C_1t_l$, et le capital restant après le deuxième mois est
    \[\bgar{ll} C_2&=C_1-(M_1-I_1)\\[.6em] &=C_1-M_1+I_1\\[.6em] &=C_1-M_1+C_1t_l\\[.6em] &=C_1(1+t_l)-M_1 \enar\]

    soit, en utilisant l'expression précédente du capital restant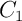 $C_1$,
    \[\bgar{ll} C_2&=C_1(1+t_l)-M_1\\[.6em] &=\Bigl[E_l(1+t_l)-M_1\Bigr](1+t_l)-M_1\\[.6em] &=E_l(1+t_l)^2-M_1\Bigl(1+(1+t_l)\Bigr) \enar\]

  • …

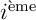  • $i^\text{ème}$ mois: en réitérant les calculs précédents, on trouve que le capital après le i-ème mois est
    \[C_i=E_l(1+t_l)^i-M_1\Bigl(1+(1+t_l)+(1+t_l)^2+\cdots+(1+t_l)^{i-1}\Bigr)\]

    soit aussi, comme la somme des termes d'une suite géométrique de raison $q\not=1$ est
    \[1+q+q^2+\cdots+q^n=\dfrac{q^{n+1}-1}{q-1}\]

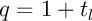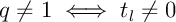    on a, avec la raison $q=1+t_l$, et $q\not=1\iff t_l\not=0$,
    \[C_i=E_l(1+t_l)^i-M_1\dfrac{(1+t_l)^i-1}{t_l}\]


Au mois $N_c$, on finit de rembourser le prêt court, et à partir du mois suivant on ne s'occupe plus que du seul prêt long restant.
Pour celui-ci, il reste alors un capital résiduel au mois $i=N_c$,
\[C_{N_c}=E_l(1+t_l)^{N_c}-M_1\dfrac{(1+t_l)^{N_c}-1}{t_l}\]

à rembourser pendant une durée résiduelle $N_R=N_l-N_c$, et ainsi avec des mensualités (de même que pour les mensualités $M_c$ du prêt court, voir partie précédente)
\[M_2=\dfrac{C_{N_c}t_l}{1-(1+t_l)^{-N_R}}\]




Il reste maintenant à déterminer l'expression, par exemple de $M_1$, pour connaître le montant de ces mensualités lissées
\[M=M_1+M_C=M_2\]

avec, d'après l'expression précédente du capital $C_{N_c}$ restant,
\[M_2=\dfrac{t_l}{(1+t_l)^{N_c}-1}\Bigl[E_l(1+t_l)^{N_c}-C_{N_c}\Bigr]\]


Maintenant, d'après le lissage $M_1+M_c=M_2$, c'est-à-dire avec l'expression de $M_2$, précédentes
\[M_1+M_C=\dfrac{C_{N_c}t_l}{1-(1+t_l)^{-N_R}}\]

et, en utlisant l'expression du capital résiduel $C_{N_c}$,
\[M_1+M_C=\dfrac{t_l}{1-(1+t_l)^{-N_R}} \Bigl[E_l(1+t_l)^{N_c}-M_1\dfrac{(1+t_l)^{N_c}-1}{t_l}\Bigr] \]

Cette expression relie les grandeurs souhaitées, il n'y a plus qu'à isoler les mensualités $M_1$:
\[\bgar{ll} &M_1\Bigl[1+\dfrac{t_l}{1-(1+t_l)^{-N_R}}\dfrac{(1+t_l)^{N_c}-1}{t_l}\Bigr] =\dfrac{t_l}{1-(1+t_l)^{-N_R}} E_l(1+t_l)^{N_c}-M_c\\[1.8em] \iff &M_1 \dfrac{(1+t_l)^{N_c}-(1+t_l)^{-N_R}}{1-(1+t_l)^{-N_R}} =\dfrac{t_l E_l(1+t_l)^{N_c}-M_c\lp1-(1+t_l)^{-N_R}\rp}{1-(1+t_l)^{-N_R}}\\[1.8em] \iff &M_1=\dfrac{t_l E_l(1+t_l)^{N_c}-M_c\lp1-(1+t_l)^{-N_R}\rp}{(1+t_l)^{N_c}-(1+t_l)^{-N_R}} \enar\]

ou encore, en multipliant numérateur et dénominateur par $(1+t_l)^{N_r}$, et comme $N_r=N_l-N_c$
\[M_1=\dfrac{t_l E_l(1+t_l)^{N_l}-M_c\lp(1+t_l)^{N_R}-1\rp} {\lp1+t_l\rp^{N_l}-1} \]

Après le calcul de $M_1$, on en déduit facilement le montant des mensualités lissées: $M=M_c+M_1=M_2$.

Domaine de validité

On imagine que dans ce type de montage, les valeurs des emprunts $E_c$ et $E_l$ ne sont pas complètement libres, sinon par exemple autant prendre immédiatement $E_l=0\iff E=E_c$, c'est-à-dire la totalité de l'emprunt sur la durée la plus courte avec le taux le plus attractif…
Plus précisément, on doit avoir $M_1>0$ (les banques parlent dans le cas contraire de prêt à rendement négatif, ce qui ne pose pas de problème d'un point de vue théorique, mais est écarté en pratique).

\[M_1>0\iff t_l E_l(1+t_l)^{N_l}-M_c\lp(1+t_l)^{N_R}-1\rp>0\]

soit, avec l'expression des mensualités du prêt court 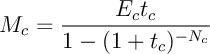$M_c=\dfrac{E_ct_c}{1-(1+t_c)^{-N_c}}$, on obtient
\[\bgar{ll} M_1>0&\iff t_l E_l(1+t_l)^{N_l}>\dfrac{E_ct_c}{1-(1+t_c)^{-N_c}}\lp(1+t_l)^{N_R}-1\rp\\[1em] &\iff \dfrac{t_lE_l}{t_cE_c}>\dfrac{(1+t_l)^{N_R}-1}{(1+t_l)^{N_l}\lb1-(1+t_c)^{-N_R}\rb} \enar\]


Ainsi le produit entre le montant du prêt long et son taux d'intérêt ne doit pas être trop petit par rapport au produit du montant du taux long et de son taux d'intérêts.

Taux global


Le calcul du taux global permet de comparer ce montage avec d'autres, en particulier avec un emprunt simple à taux fixe.
Le calcul est celui explicité là Lien, tandis que l'outil suivant permet de le calculer pratiquement, et automatiquement .

Généralisation: lissage de n prêts


\[\psset{unit=1cm,arrowsize=10pt} \definecolor{g4}{gray}{0.4} \definecolor{g5}{gray}{0.5} \definecolor{g6}{gray}{0.6} \definecolor{g7}{gray}{0.8} \begin{pspicture}(-1.4,-1.6)(14.2,8.8) \pspolygon[fillstyle=solid,fillcolor=g7](0,0)(13,0)(13,7.5)(0,7.5) \pspolygon[fillstyle=solid,fillcolor=white](0,0)(10.5,0)(10.5,6.5)(0,6.5) \rput(8.6,3){$\dots$}\rput(2,5.5){$\dots$}\rput(5.6,5.5){$\dots$} \pspolygon[fillstyle=solid,fillcolor=g6](0,0)(7.5,0)(7.5,4.5)(0,4.5) \pspolygon[fillstyle=solid,fillcolor=g5](0,0)(6,0)(6,3.5)(0,3.5) \pspolygon[fillstyle=solid,fillcolor=g4](0,0)(4,0)(4,2.5)(0,2.5) % \rput(-.25,-.25){0} \psline{->}(-.35,0)(-.35,2.5)\rput[r](-.5,1.5){$M_1$} \psline{->}(-.35,1.52)(-.35,3.48) \rput[r](-.5,3.){$M_2$}\psline(-.2,3.5)(0,3.5) \psline{->}(-.35,3.52)(-.35,4.48) \rput[r](-.5,4){$M_3$}\psline(-.2,4.5)(0,4.5) \psline{->}(-.35,4.52)(-.35,5.4) \rput[r]{90}(-.36,6.2){$\dots$} \psline{->}(-.35,6.52)(-.35,7.48) \rput[r](-.5,6.8){$M_n$}\psline(-.2,7.5)(0,7.5) % \psline(4,0)(4,-.2)\rput(4,-.5){$N_1$} \psline{->}(0,-.9)(3.98,-.9)\rput(2,-1.3){$\Delta_1=N_1$} \psline(6,0)(6,-.2)\rput(6,-.5){$N_2$} \psline{->}(4.02,-.9)(5.98,-.9)\rput(5,-1.3){$\Delta_2$} \psline(7.5,0)(7.5,-.2)\rput(7.5,-.5){$N_3$} \psline{->}(6.02,-.9)(7.48,-.9)\rput(6.8,-1.3){$\Delta_3$} \psline(10.5,0)(10.5,-.2)\rput(10.5,-.5){$N_{n-1}$} \psline{->}(10.52,-.9)(12.98,-.9)\rput(11.8,-1.3){$\Delta_n$} \psline(13,0)(13,-.2)\rput(13,-.5){$N_n$} \psline[linewidth=1.8pt]{->}(-.2,0)(14,0) \psline[linewidth=1.8pt]{->}(0,-.2)(0,8.5) \end{pspicture}\]


Accéder directement à l'outil de calcul/calculette en ligne pour le calcul des mensualités lissées
On note pour chaque emprunt, comme illustré sur le graphique précédent,
  • $E_i$, le montant du i-ème emprunt
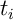  • $t_i$, le taux d'intérêts mensuel du i-ème emprunt
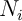  • $N_i$, la durée, en mois, du i-ème emprunt


Pour les deux premiers emprunts, on se retrouve dans la situation précédente.
Les mensualités pour le premier emprunt sont alors
\[M_1=\dfrac{E_1t_1}{1-(1+t_1)^{-N_1}} \]

et pour le second, les mensualités $M_2$ sont,
\[M_2=\dfrac{t_2 E_2(1+t_2)^{N_2}-M_1\lp(1+t_2)^{\Delta_2}-1\rp} {\lp1+t_l\rp^{N_2}-1} \]

puis la première mensualité lissée, $M_2'=M_1+M_2$.


Ensuite, en ayant lissé ces deux premiers emprunts, on se retrouve dans la situation précédente à nouveau: on "emboîte" dans le troisième emprunt $E_3$ ce premier "emboîtement" lissé $M_2'$, pour lequel
\[ M_3=\dfrac{t_3E_3(1+t_3)^{N_3}-M_2'\lp (1+t_3)^{\Delta_3}-1\rp}{(1+t_3)^{N_3}-1} \]

On obtient ainsi le nouveau lissage, pour ces trois premiers prêts, $M_3'=M_1+M_2+M_3=m_2'+M_3$, ce qui nous permet de calculer de même le lissage pour le quatrième prêt dans lequel on peut emboîter ces trois premiers, et ainsi de suite …

Calculette en ligne pour le calcul des mensualités lissées


LongPage: h2: 4 - h3: 3