Réseaux de neurones

L'imagination est une capacité fondamentale à l'activité intellectuelle humaine. Elle est à la source de toute découverte, scientifique ou autres.

De tous temps l'homme a puisé dans son imagination pour tenter de connaître, et par la suite de maîtriser, son environnement naturel, que ce soit au travers de mythes, de croyances diverses et de religions, de superstitions, ou plus récemment de preuves scientifiques.

Ces diverses croyances ne s'auto-excluent pas pour autant, elles sont au contraire liées entre elles. D'après Wittgenstein [3], "nous ne pouvons nous représenter aucun objet en dehors de la possibilité de sa liaison avec d'autres", et Changeux de compléter [3]: "les objets s'imbriquent les uns dans les autres comme les éléments d'une chaîne et le déroulement de cette chaîne constitue, en définitive, la pensée."

Néanmoins, au cours du vingtième siècle, le courant du positivisme logique, émanant du cercle de Vienne, s'est donné pour objectif l'élimination de toutes les hypothèses et idées métaphysiques dans les sciences. La science a voulu se débarrasser définitivement de sources d'imagination extérieures. Les idées restent néanmoins denrées rares et recherchées, et mènent souvent encore à des découvertes décisives. Pour Karl Popper [1] "[en parlant de la métaphysique] ses idées sont ce que l'homme a de plus précieux. Nous n'avons jamais assez d'idées. Nous souffrons en permanence d'une pénurie d'idées. Et les idées constituent un bien si précieux qu'il faut traiter avec respect la métaphysique et en discuter avec déférence - peut-être sortira-t-il quelque chose de ces idées.
Bien sûr, et c'est là le problème, d'abord nous n'avons pas assez d'idées, ensuite, d'une façon générale, leur discussion ne donne pas grand chose, parce que nous n'avons pas assez d'idées pour la critique des idées."

Le larouse (1988) donne deux définitions du verbe imaginer: se représenter quelque chose dans l'esprit, et, trouver un nouveau moyen, inventer quelque chose, c'est-à-dire créer une chose originale ou nouvelle à laquelle personne n'avait pensé.
Nous allons voir que ces deux définitions sont en fait très liées, que l'imagination au sens de création d'une nouveauté débute par l'imagination au sens de la représentation mentale d'objets.

Surtout, nous verrons que le terme de création employé est critiquable car il s'agit plus, à proprement parler, de processus de restructuration, de réagencement, d'association, de combinaison et de modification de représentations déjà existantes. En d'autres termes, même dans ce domaine de l'esprit, si des éléments peuvent se perdrent (plus précisément, peuvent s'oublier), "rien ne se créé, tout se transforme".

Dans un premier temps, nous commençons par décrire brièvement le fonctionnement biologique des cellules nerveuses, le neurone pris isolément tout d'abord, puis imbriqué dans une structure plus complexe, dans un réseau de neurones. Ceci nous permettra de fournir un modèle connexionniste des représentations mentales, et ainsi de comprendre comment celles-ci peuvent être reliées entre elles d'une part, et d'autre part, comment de nouvelles peuvent "apparaître".

La modélisation de phénomènes en réseau est très riche, et n'est pas restreinte strictement aux réseaux de neurones et aux représentations mentales. Les études et théories antérieures sur le sujets sont nombreuses et permettent d'éclairer et d'apporter des éléments pertinents sur le sujet. C'est le cas de la théorie mathématique des graphes, ainsi que de la théorie de la percolation. Ces théories, leurs liens et leurs apports en termes de représentations mentales, seront alors succintement évoquées.

Enfin, on s'efforcera de faire ressortir chaque fois que possible, des éléments applicatifs des notions rencontrées en termes d'apprentissage et de pédagogie.

Neurones et réseaux de neurones biologiques

Le cerveau est un des objets matériels le plus complexe que l'on connaisse. C'est sans nul doute en son sein que se situent les divers mécanismes liés à l'intelligence humaine: analyse des perceptions, réflexion, mémoire, et aussi, à la lumière des avancés récentes en neuroscience, la conscience (c'est un propos central chez Edelman, [2]).

Une grande variété de structures cérébrales ont à l'heure actuelle été identifiées, à des échelles qui vont de la molécule aux neurones et à des régions toutes entières.
La description précise de ces structures sort largement du propos de ce texte (et des connaissances de l'auteur), on pourra se référer à, par exemple, [2], [3], [5]. Néanmoins, la description d'une cellule cérébrale, et plus particulièrement de son fonctionnement lorsque nombre d'entre elles sont interconnectées, semble incontournable pour la compréhension des principaux phénomènes qui nous intéressent: le neurone.

Cette description sera délibérement brève (donc sûrement aussi quelque peu simpliste), et s'attachera principalement à la description d'une théorie "neurale" permettant d'appréhender les phénomènes généraux liés à l'intelligence humaine.

Neurone biologique

Le cerveau humain possède environ trente milliards de neurones, reliés entre eux par un million de milliards de connexions.

Un neurone consiste en un corps cellulaire dont le diamètre est de l'ordre de trente microns (trente millièmes de millimètre). Ces cellules sont polaires; elles comportent un ensemble arborescent d'extensions appelées dendrites d'une part, ainsi que d'autre part une longue extension spécialisée, dite axone, qui le connectent à d'autres neurones par le biais de synapses.
Le neurone est une cellule spécialisée dont l'activité est essentiellement électrique (ou plus précisément électro-chimique). Ces courants sont évidemment interprétés différemment selon l'organe qui les reçoit: les muscles se contractent, les glandes secrétent des substances chimiques, et les autres neurones les intégrent pour produire éventuellement d'autres courants. Un neurone émet un signal en fonction des signaux qui lui proviennent des autres neurones. On observe en fait au niveau d'un neurone, une intégration des signaux reçus au cours du temps, c'est à dire une sommations des signaux (c'est une intégration au sens mathématique). En général, quand la somme dépasse un certain seuil, le neurone émet à son tour un signal électrique.

La notion de synapse explique la transmission des signaux entre un axone et une dendrite. Au niveau de la jonction (c'est à dire de la synapse), il existe un espace vide à travers lequel le signal électrique ne peut pas se propager. La transmission se fait alors par l'intermédiaire de substances chimiques, les neuromédiateurs. Quand un signal arrive au niveau de la synapse, il provoque l'émission de neuromédiateurs qui vont se fixer sur des récepteurs de l'autre côté de l'espace inter-synaptique. Quand suffisamment de molécules se sont fixées, un signal électrique est émis de l'autre côté et on a donc une transmission. Suivant le type de la synapse, l'activité d'un neurone peut renforcer ou diminuer l'activité de ces voisins. On parle ainsi de synapse excitatrice ou inhibitrice.

En plus de la nature de la connexion, la dynamique temporelle est à prendre en considération. En effet, après excitation et transmission d'un signal par un neurone, celui-ci admet une période d'inhibition pendant laquelle la cellule ne peut pas traîter d'autres éventuels signaux reçus. Cette période d'inhibition semble d'autant plus marquée que l'excitation qui la précéde provient d'une connexion forte.

Un neurone seul est insuffisant pour remplir une fonction particulière (par exemple de perception). Pour ce faire, de très nombreux neurones interconnectés, formant alors un réseau de neurones, sont nécessaires.

Réseau de neurones

Pour expliquer, à partir de réseaux de neurones, des fonctions telles que la mémorisation, l'apprentissage, l'imagination, ... ou plus généralement, l'ensemble des objets mentaux, la notion de "résonateurs en boucle" [4] semble probante. On la retrouve sous la désignation de "cartes mentales" chez Edelman [2], ou encore avec la notion de graphe et de sous-graphe chez Changeux [3].

Un exemple de tel réseau de neurones est schématisé sur la figure

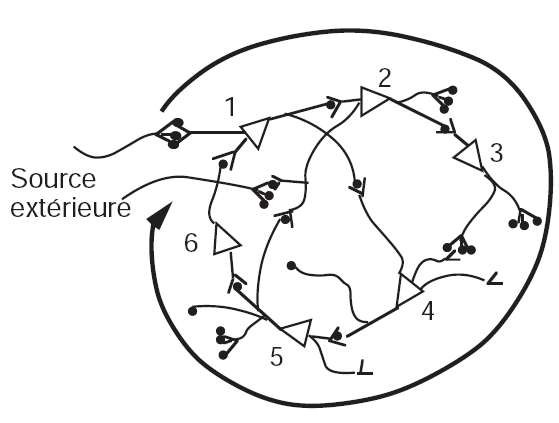
Un signal extérieur est transmis aux neurones 1 et 2, qui le propagent ensuite vers les neurones 2 et 4. Par exemple, le neurone 4 peut ne pas être suffisament excité pour transmettre à son tour un signal (effet d'intégration des signaux afférents introduit précédemment, son seuil n'est pas atteint), mais il va néanmoins être supplémentairement excité par l'intermédiaire du neurone 3, lui-même alimenté par le neurone 2. Ensuite, l'activation est propagée par les neurones 5, puis 6, qui permettent de ``boucler'' le signal sur les neurones 1 et 2 de départ.

Lecerf [4] parle à ce titre de "boucle auto-reproductrice", ou de circuit résonateur; nous reviendrons plus précisément sur cette notion ultérieurement. Ceci permet d'expliquer les phénomènes de mémorisations et autres objets mentaux.

Rappelons tout d'abord la loi de Hebb, relative à la force d'une connexion entre deux neurones: un neurone renforce d'autant plus une connexion qu'elle conduit à son activation. Chaque cellule tend localement à augmenter l'efficacité de ses connexions actives, donc à maintenir les conditions régulières de son activité. En d'autres termes, chaque neurone tend à stabiliser son fonctionnement "le plus courant".

Imaginons maintenant que, dans l'exemple schématisé sur la figure [*], la stimulation extérieure soit maintenue pendant un certain temps, suffisament pour que l'activation ``en boucle'' des six neurones s'auto-entretienne. Alors, chacun de ces neurones étant simultanément actifs, les connexions les reliant vont se renforcer. De là, une simple excitation extérieure activant le neurone 1 (par exemple, ou un des cinq autres), va directement activer le neurone 2 à la suite, la connexion entre les deux étant devenue relativement forte, et ainsi de suite tout au long de la chaîne. Cette dernière est donc devenue stable (elle va pouvoir perdurer dans le temps car il faudra dès lors une certaine durée d'inactivité pour que les connexions reperdent leur efficacité) et facilement activable.

Ce modèle permet d'expliquer par exemple la mémorisation d'une perception: plus un individu est soumis à la même stimulation, plus celui-ci la mémorise fortement; en fait, plus une certaine boucle, ou sous-graphe de neurones, se renforce et se stabilise et devient facilement ré-activable.

Phénomène de résonance

La terminologie de "résonance", empruntée aux sciences physiques, est souvent utilisée pour désigner et expliquer la stabilisation d'un réseau de neurones. Ce point mérite d'être détaillé. La notion de résonance en physique est attachée à celle d'oscillateur, ou de système oscillant. Le système tel que schématisé figure [*] peut éventuellement se comporter comme un système oscillant: chaque neurone a une période propre d'activité et d'inactivité, ainsi l'activation successive et bouclée des neurones se comporte alors comme la propagation d'une onde auto-entretenue dans un milieu. Chaque réseau de neurones, suivant le nombre de neurones qui le constitue ainsi que leurs caractéristiques physiques propres, aurait ainsi une fréquence propre, ou fréquence de résonance. Un message nerveux, provenant soit d'un organe de perception soit d'un autre réseaux de neurones, arrivant sur ce réseau à cette fréquence particulière exciterait alors "au mieux" le réseau. Inversement, ce réseau serait alors quasiment insensible à toute excitation de fréquence différente.

Cette modélisation par un comportement oscillant de réseaux de neurones constitue encore à l'heure actuelle un modèle purement théorique.
En effet, ces états d'activité corrélés d'un réseau de neurones n'ont, pour l'instant, jamais été mesurés avec précision. Seuls des états d'activités de régions du cortex cérébral ont été observés chez l'homme à l'aide de caméras à positrons. Ces observations montrent que les neurones actifs, même suite à une stimulation simple, se répartissent dans diverses régions distinctes de l'encéphale, et peuvent donc être relativement éloignés les uns des autres. L'activité neuronale cérébrale s'effectue sûrement en réalité suivant des réseaux de réseaux de neurones.

La notion de réseau a été étudiée bien auparavant celle spécifique de réseau de neurones, avec, par exemple, les réseaux d'atomes d'un matériaux (cristallographie), les réseaux de télécommunications, ... Son étude abstraite conduit à la théorie des graphes, qui, à son tour, délivre des éléments d'étude pertinents pour les réseaux de neurones.

Théorie des graphes

Nous concernant, les sommets sont simplement les neurones tandis que les arcs représentent les connexions synaptiques entre neurones.

La théorie des graphes fournit les éléments pertinents à étudier dans le vaste réseau neuronal cérébral. En effet, la théorie des graphes étudie sur de tels objets, des notions telles que celle de chemin (s'il existe, liste des arcs successifs reliant deux sommets), de boucle (chemins parcourant au moins deux sommets identiques), de chemins parallèles (chemins différents ayant les mêmes extrémités), pour ne citer que les principales.

Les notions de chemin et de boucle ont été introduites précédement; la notion de parallèlisme est très centrale chez Edelman (qui propose la qualification de "redondance", ou "dégénerescence") qui y base un des trois piliers de sa "théorie de la sélection des groupes de neurones" [2].

A l'intérieur d'un graphe complet, on peut définir des sous-graphes, ou sous-réseaux; ceux-ci vont correspondrent à la notion de carte mentale introduite par Edelman [2], ou de boucle pour Lecerf [4], tandis que Changeux [3] se satisfait quant à lui très bien de la terminologie mathématique de graphe et sous-graphe.

Dans un graphe, sans parallèlisme (sans redondance des chemins), on peut avoir, au maximum 4#4 arcs ou chemin. Ainsi, à partir d'une trentaine de milliard de neurones, on pourrait avoir jusqu'à environ neuf cents milliards de milliards de connexions différentes, à comparer au nombre réel estimé légérement plus faible de un million de milliards de connexions: tous les neurones ne sont pas nécessairement interconnectés entre eux, d'autant plus que certains le sont de multiples fois (il y a justement du parallélisme dans le vaste réseau de neurones de l'homme).

Enfin, dans un graphe contenant n sommets, on peut dénombrer jusqu'à 2ⁿ sous-graphes. Ainsi, si on accepte qu'un objet mental se confonde avec un sous-réseau ou sous graphe neuronal, alors, avec notre trentaine de milliards de neurones, on doit être en mesure de former quelques 10¹⁰¹⁰ (soit un nombre qui s'écrit avec un "un" suivi de dix milliards de zéros) objets mentaux distincts.

Cela munit l'homme de capacités cérébrales gigantesques, et permet ainsi de modéliser et d'expliquer de nombreux phénomènes mentaux tels que ceux d'apprentissage et de mémorisation. Au delà même de ces capacités mentales, cette modélisation donne les bases d'une explication scientifique de la conscience. C'est le point de vue soutenu par Edelman [2], ainsi que Changeux [3], qui s'oppose à la notion d'"émergence", introduite par le courant connexionniste.

Changeux conclut à ce sujet par [3]: "Doit-on dire que la conscience "émerge" de tout cela ? Oui, si l'on prend "émerger" au pied de la lettre, comme lorsqu'on dit que l'iceberg émerge de l'eau. Mais il nous suffit de dire que la conscience est ce système de régulation en fonctionnement. L'homme n'a dès lors plus rien à faire de l'"Esprit", il lui suffit d'être un Homme Neuronal".

Représentations mentales

Le modèle physico-biologique de réseaux neuronaux introduit précédemment permet d'aborder la notion de représentation mentale.

En effet d'après ce qui précède, une représentation mentale correspond à l'activation simultanée, voire l'entrée en résonance, d'un réseau de neurones.

Dans la terminologie "traitement de l'information" et "traitement du signal", le déclenchement de l'activité cérébrale se fait par la propagation d'un signal (électro-chimique) dans l'immense réseau de neurones de l'encéphale. Ce signal initial peut par exemple provenir d'un stimulus extérieur, après transformation par un organe spécifique du corps d'une excitation extérieure (mécanique, photo-électrique, thermique,...) en influx nerveux.

Ce signal nerveux se propage alors dans le graphe complet de neurones, au gré des connexions existantes entre les différents neurones rencontrés. Ce signal peut alors faire entrer en "résonance" un sous-réseau, ou sous-graphe, neuronal tel que nous l'avons décrit précédemment.

A partir de ce moment là, à moins que déjà antérieurement, le stimulus est attaché à ce réseau particulier: à chaque exposition à ce stimulus, ce réseau sera activé et sa cohésion renforcée. D'une certaine façon, le stimulus a été mémorisé.

Une caractéristique principale de l'homme, le différenciant ainsi d'un grand nombre d'autres espèces animales, et sa capacité, en l'abscence de stimulus extérieur, à activer un réseau précis neuronal: en d'autres termes, la capacité à penser intérieurement à des évènements qui n'ont pas ou plus réellement lieu ¹.

Ainsi, l'homme peut se représenter ``mentalement'' des éléments réels, même en leur abscence. Il est intéressant de noter de plus que l'activité neuronale d'un individu soumis à une situation particulière est identique à celle en l'abscence du contexte extérieur. Ce fait est en particulier largement exploité par les sportifs de haut niveau, qui y trouvent ainsi une méthode de préparation "intérieure", simulant en quelques sortes les actions réelles [7].

Liens entre représentations mentales

Nous avons vu jusqu'à maintenant, la modélisation d'un objet mental, en tant que sous-réseau, sous-graphe, de l'ensemble de la population de neurones. Le nombre théorique de tels sous-graphes différents que l'on peut former est gigantesque. Pour que ceci soit possible, il faut bien se rendre compte que les sous-graphes ainsi formés sont entremélés: des neurones peuvent appartenir à plusieurs sous-graphes disctincts.

Ce fait implique la conséquence suivante. Lors de la représentation mentale d'un objet (réel ou conceptuel), un sous-graphe neuronal est activé, c'est-à-dire qu'une chaîne d'excitation se propage, en boucle et de manière stable, le long des neurones qui le forme. Maintenant, si un ou plusieurs neurones appartiennent aussi à un autre sous-graphe distinct, alors l'activation de ces neurones peut aussi, potentiellement, entrainer celle des autres sous-graphes les contenant.

Ceci explique le phénomène "d'association d'idées": penser à quelque chose peut, dans certain cas, évoquer chez un individu le souvenir d'autre chose, même parfois sans lien sémantique ni sémiotique².

Inversement, on se rend compte qu'il est d'autant plus facile d'apprendre un élément que celui-ci se ``rapproche'' (nous reviendrons ultérieurement sur cette notion de proximité) de connaissances précises et déjà bien ancrées. En effet, d'un point de vue neuronal, il est plus facile de modifier légèrement un sous-graphe existant, voire de seulement y ajouter quelques connexions et neurones, plutôt que d'en créer un complètement nouveau.

Ce fait constitue un élément de base en pédagogie: rechercher à s'appuyer sur des connaissances, les plus solides possibles, antérieurement acquises afin d'amener une notion nouvelle. On peut aussi de plus interpréter la notion "de sens" que l'on donne à une nouveauté que l'on cherche à apprendre ou à enseigner.

Une nouveauté a du sens si elle s'intégre dans un réseau ancien et qui possède donc déjà une certaine cohésion. Dans ce cas, l'apprentissage de de cette nouveauté se fait par enrichissement des structures déjà fortes et existantes.

Sans ce "sens" que l'on peut donner, on est ainsi contraint à développer un structure neuronale nouvelle et donc indépendante des autres. Cette structure est pour l'instant très faible, et il faudra une certaine insistance pour la renforcer, c'est-à-dire pour intégrer pleinement et pour un long terme cette nouveauté.

De la perception à la conceptualisation - Processus d'abstraction

Avec cette modélisation neuronale à l'appui, tout objet mental se réduit à l'activité d'un sous-graphe neuronal spécifique, et ce, que l'objet en question provienne de perceptions (monde sensible) ou soit purement subjectif. Le passage de l'image physique et sensible au concept peut alors se voir en deux étapes. La première consiste à l'élagage des composantes sensorielles: le sous-graphe neuronal peut-être consciemment activé par un individu en l'abscence même de perceptions sensorielles. La deuxième étape se fait ensuite par enrichissement combinatoire et enchaînement d'objets mentaux. Cette deuxième étape est rendue possible par la première: bien que des perceptions réelles peuvent ne concorder en aucun point, leur sous-graphe neuronaux ne sont pas pour autant complètement disjoints...

En pédagogie, ceci montre l'intérêt des exemples et autres métaphores, c'est-à-dire de l'image apportée à l'élève pour la construction mentale d'un concept. Cette image peut-être grandement nécessaire pour lui permettre de se créer ses propres représentations mentales concernant l'objet en question. L'image doit ainsi par la suite être retirée (plus ou moins rapidement) pour pouvoir alors lui permettre de la conceptualiser, c'est-à-dire de laisser place à sa propre représentation mentale, puis enfin, de la relier à d'autres objets.

D'une manière plus générale, la construction de concepts, selon Skemp (1971) (cf. [9]), et de concepts mathématiques en particulier, s'effectue en deux temps: - l'abstraction, activité au moyen de laquelle nous arrivons à être conscients des similitudes, et - la classification, activité qui nous permet de rassembler nos expériences sur la base de ces similitudes.

Processus de création de nouvelles représentations mentales - Imagination

Plasticité des réseaux neuronaux

Dans un sous-graphe neuronal, par exemple le schéma simplifié figure [*], si seulement certains neurones sont excités par une stimulation extérieure, par exemple, les neurones 1, 3 et 5, le sous-graphe complet formé des neurones de 1 à 6 a de grande chance d'être activé. Le sous-graphe complet a d'autant plus de chances d'être totalement activé que les connexions entre les différents neurones sont déjà fortes, c'est-à-dire que l'objet mental correspondant est familier.

En d'autres termes, une stimulation partielle, vis-à-vis d'une stimulation familière plus globale, permet à elle seule de conduire à un même objet mental: la stimulation habituelle complète est reconstituée.
Par exemple, la présentation d'une suite de mots auxquels un certain nombre de lettres ont été retirées à un lecteur familier du vocabulaire utilisé ne posera aucun problème de lecture et de compréhension à ce dernier. Plus encore, le lecteur pourra même ne pas s'apercevoir de la supercherie.

Dans le modèle de réseau neuronaux, les mots familiers sont en correspondance avec des objets mentaux, qui sont des sous-graphes ou réseaux restreints de neurones. Les connexions entre les neurones sont d'autant plus fortes que les mots utilisés sont familiers (loi de Hebb).
Par la suite, la présentation d'un mot auquel on a retiré une lettre active un certain nombre de neurones du sous-graphe correspondant au mot complet, puis, rapidement le sous-graphe complet: le mot complet est reconstitué. Avec un vocabulaire globalement familier, il faut une réelle concentration de la part du lecteur pour s'apercevoir de ce genre d'erreur. Cela peut expliquer notamment les difficultés rencontrées lors de la chasse aux "erreurs de frappe" dans un document dactylographié.
D'une manière plus générale, un stimulus extérieur complexe est décomposé puis analysé simultanément en diverses régions du cerveau; la synthèse globale du signal perçu ne s'effectue qu'ultérieurement, après réassemblage. En d'autres termes, on a affaire à des réseaux de réseaux de neurones pour constituer un objet mental complexe.

Prenons l'exemple d'une image. Des études ont montré que le traitement par le cortex visuel primaire d'une telle image est effectué localement, fragment par fragment. L'assemblée de neurones en charge du traitement de cette image ne procède pas à un découpage purement géométrique, mais détectent des patterns, des structures et formes "courantes".
Ceci permet d'une part de comprendre comment le cerveau arrive à reconnaître, à l'intérieur même d'une image, certains éléments connus.
Par ailleurs, d'autre part, il devient tout à fait possible pour un individu d'effectuer la synthèse personnelle de l'image. Ayant dissocié et reconnu les différentes composantes d'une image (celles-ci constituent alors des objets mentaux, abstraits de leur contexte physique initial), il devient possible de recomposer une image, mentalement, avec divers objets mentaux choisis à la convenance de l'auteur. Une nouvelle représentation mentale est née, qui, si elle était fidèlement transposée physiquement (sur une toile par exemple, là intervient pour une grande part le talent de l'artiste), serait un pur produit de l'imagination de l'auteur.

Percolation d'un message nerveux

Nous avons vu que la création de nouvelles représentations mentales pouvaient naître de l'''association'' de certaines d'entre elles plus anciennes. L'excitation d'un ou plusieurs neurones à l'intérieur d'un sous-graphe neuronal déjà indentifié peut aboutir à l'activation du sous-graphe complet, donc de l'objet mental correspondant.
En ces termes, étudier l'éventualité de l'association d'idées distinctes, c'est-à-dire l'activation corrélée de sous-graphes distincts (ayant éventuellement des neurones communs) revient à étudier la possibilité pour qu'un signal nerveux provenant d'un des deux sous-graphes atteigne l'autre, puis l'active.

L'étude de la possibilité de la propagation d'un signal dans un réseau a auparavent été faite dans un contexte nettement différent. La question principale était, dans un contexte militaire: dans un réseau de communication donné (le réseau de télécommunication d'un pays en l'occurence), quel pourcentage de relais de transmission faut-il détruire pour qu'un signal partant d'un certain point géographique ne puisse pas en atteindre un second ?
En effet, la suppression d'un relai n'empêche pas nécessairement la transmission du signal qui pourrait alors transiter par d'autres voies détournées, de même pour la suppression de deux, trois... relais.

Cette étude a donné lieu à la théorie de la percolation, qui a permis, entre autre, de mettre en évidence l'existence d'un seuil, dit seuil de percolation, au delà duquel, en probabilité, la communication devient impossible entre deux points quelconques distincts du réseau global. Cela donnait, en termes militaires, le nombre minimum de relais à détruire pour paralyser tout moyen de communication de l'ennemi.

L'analogie avec les réseaux de neurones de l'encéphale est grande, pour lesquels chaque neurone joue le rôle de relai. Malheureusement, encore à l'heure actuelle, il reste impossible d'obtenir la carte complète des relais (les neurones) et de leurs inter-connexions pour pouvoir y appliquer directement ce genre de théorie, et pouvoir déterminer ainsi directement la probabilité pour que deux sous-graphes, c'est-à-dire deux objets mentaux, soient "reliables".

La possibilité de la discrimination de deux stimuli distincts par un individu est un sujet d'étude et de recherche relativement ancien. On recherche dans ce cadre à déterminer quand un individu soumis à deux stimulations "proches", mais néanmoins différentes, va être en mesure de les différencier ou non.
Dans cette étude, la mesure (très théorique jusque là) de l'écart entre les stimuli est le point clé: la définition mathématique d'une distance est l'objet central recherché permettant de quantifier l'écart entre deux stimuli. Ensuite, grossièrement, on peut définir un seuil en deçà duquel les stimuli ne peuvent être distingués l'un de l'autre par un individu car ils sont alors "trop proches" l'un de l'autre, et au delà duquel ils apparaîtront comme bien différents (cf. [6]).

La modélisation neuronale, associée à celle d'objets mentaux, permet premièrement d'affirmer que la distance, indépendamment de sa définition, entre les stimuli importe en réalité peu; chaque stimulus correspond à un objet mental spécifique, c'est-à-dire à un sous-graphe neuronal: c'est la proximité entre ces deux sous-graphes qui est essentielle (la proximité, ou distance, en théorie des graphes est définies comme la plus petite distance à l'intérieur du réseau permettant de joindre deux sommets, ou deux sous-graphes).

Quelques éléments pratiques permettant d'imaginer, ou de faire imaginer

Pour un élève, l'imagination est une compétence requise à chaque instant dès lors que l'enseignement se veut porter sur des éléments nouveaux, nouveaux pour l'élève. L'imagination est bien à prendre ici au sens ou nous l'avons décrit jusque là: il ne s'agit pas de "nouveautés absolues", mais de connaissances s'appuyant sur d'autres acquises antérieurement. Un enjeu adapté vis-à-vis de ce qui précède est alors, dans de telles situations de nouveauté apparente pour l'élève, de fournir les moyens de s'appuyer au mieux sur ses structures mentales déjà disponibles et si possible qu'il a déjà largement éprouvées, la force des sous-graphes neuronaux correspondant n'en étant alors que plus forte.

Pour ce faire, il peut être bon de rechercher à créer "du lien" pour l'élève. Imaginons que l'on suppose que l'élève ait une représentation correcte d'un élément 8#8 et que, à partir de celui-ci, on souhaite lui faire apprendre, ou découvrir, un élément 9#9. En termes neuronaux, il s'agit de faire parcourir, voire créer, un lien entre les sous-graphes correspondant aux objets mentaux 8#8 et 9#9. Ceci n'est pas forcément une tâche aisée; le chemin peut-être long (au sens propre du terme). Il peut alors être bon d'aider l'élève en lui introduisant un élément 10#10 intermédiaire, plus facilement accessible à partir des éléments 8#8 et 9#9. Malheureusement (ou bienheureusement), la carte mentale d'un individu, d'un élève entre autre, n'est pas visible par un autre individu (du moins encore à l'heure actuelle, avec les moyens techniques que l'on dispose). Il peut-être bon alors d'interroger directement l'élève, avec des questions simples du type: ``à quoi te fait penser ceci'', de manière à pouvoir se donner une idée de l'élément 10#10 intermédiaire à introduire.

En cas d'échec à trouver un élément 10#10 intermédiaire adapté, la dimension stochastique des phénomènes neuronaux n'est pas non plus à négliger. Des connexions se créent à tout instant aléatoirement, et la probablité pour que le lien recherché se créer "spontanément" n'est pas nulle³. C'est pourquoi, après avoir longuement cherché un problème sans succès, il peut-être bon de changer complètement de registre, de laisser passer quelques temps, avant de se relancer dans la recherche.

L'erreur des élèves acquiert aussi un statut particulier. Si dans certains cas, celle-ci peut-être un vecteur de progrès, il faut néanmoins la considérer avec méfiance.
Face à un problème nouveau, un élève peut réfléchir et proposer une méthode ou solution erronée. Dans ce cas, l'élève a développé par lui-même ses structures neurales (association, combinaison, structuration de sous-graphes neuronaux) avec des liaisons fortes si l'élève a vraiment cherché et réfléchit par lui-même. Il devient alors assez simple de corriger ces erreurs, les structures fortes qu'il a mis en place ne sont plus qu'à modifier, une base importante est là.

Le problème est différent si une donnée nouvelle et erronée est simplement proposée à un élève (ou, en fait, à tout individu). C'est le cas courant, par exemple, des QCM. En l'abscence de la connaissance précise de la réponse à une question, l'élève peut-être amené à choisir une réponse quelque peu aléatoirement. Ainsi, il a sous les yeux, une image associant deux idées: une question et sa réponse fausse, et met en place des structures neuronales correspondantes, faibles certes mais qui existeront quelques temps durant. Alors, apporter la réponse exacte à la question par la suite et sans explications conséquentes, comprises et intégrées par l'élève, reviendra à tenter de modifier faiblement une structure déjà faible. Au final, il reste une probabilité non négligeable (voire même prépondérante) que l'association perdure entre la question et la réponse inexacte fournie en premier lieu.

Dans un autre registre, les disciplines artistiques sont reconnues pour être "très gourmandes" en imagination. D'un autre côté, les disciplines requérant un fort niveau d'abstraction (telles que les mathématiques, ou les sciences en général) demandent, en fin de compte, la même compétence. En effet, dans le premier cas, l'artiste s'efforce sans cesse de créer de la nouveauté comme simples associations et restructurations de ses représentations mentales personnelles; chaque spectateur de l'11#11uvre d'art ayant sa propre biographie, et donc ses propres représentations mentales, a priori bien distinctes de celles de l'artiste, y perçoit alors quelque chose de nouveau pour lui, quelque chose qui a été créé de toute pièce.
Déjà pour une personne évoluant dans le même milieu que l'artiste, ou ayant un vécu proche, la nouveauté est plus discutable.

En ce qui concerne les disciplines abstraites, l'abstraction ayant supprimer le lien d'avec le réel, le monde perçu, l'activité intellectuelle consiste à trouver, voire créer, des liens entre objets mentaux distincts. En d'autres termes, un besoin comparable en imagination est requis.

La différence fondamentale persistante entre art et sciences, à ce niveau là, et que si l'artiste peut créer librement, c'est-à-dire sans aucune contrainte autre que l'esthétique final de son 11#11uvre, le scientifique ne peut le faire qu'en respectant les règles du système dans lequel il se situe (règles logiques et plus généralement mathématiques, lois physiques éprouvées...).

Bibliographie

1

Konrad Lorentz, Karl Popper, L'avenir est ouvert, Flammarion, 1995.

2

Gerard Edelman, Plus vaste que le ciel, une nouvelle théorie générale du cerveau, Odile Jacob, 2004.

3

Jean-Pierre Changeux, L'homme neuronal, Hachette: Pluriel sciences.

4

Christophe Lecerf, Une leçon de piano ou la double boucle de l'apprentissage cognitif, Travaux et documents, Université Paris 8, 1997.

5

Jacques-Michel Robert, Le cerveau, Dominos, Flammarion, 1994.

6

Ehtibar N. Dzhafarov, Multidimensional Fechnerian Scaling: Probability-Distance Hypothesis, Journal of Mathematical Psychology, 46, pp. 352-374.

7

S. Vieilledent, G. Dietrich, A. Berthoz, Etude de la représentation mentale de trajets locomoteurs: l'exemple de l'escalade sportive, Sciences and Sports, Vol. 12, pp. 33s-34s, 1997.

8

P. Jacob, Neurones miroir, résonance et cognition sociale, Psychologie française, 52, pp. 299-314, 2007.

9

Fernando Hitt, Les représentations sémiotiques dans l'apprentissage de concepts mathématiques et leur rôle dans une démarche heuristique, Revue des sciences de l'éducation, Vol. XXX, n12#12 2, pp. 329-354, 2004.

... lieu ¹

Une catégorie particulière de neurones, dits neurones miroir, a été récemment identifiée qui serait à l'origine de cette capacité, très spécifique à l'homme (voire par exemple [8]).

... sémiotique ²

L'association d'idée constitue un des fondements de la technique d'analyse psychanalytique introduite par Freud.

... nulle ³

Cette idée a été initialement introduite par Ross Ashby pour des sytèmes dits à "auto-organisation". On peut voir en effet l'homme comme un tel système auto-organisé; dans cette visée, l'ensemble des connexions internes de l'homme sont en mesure de se modifier aléatoirement, en vue d'une meilleure adaptation du système global à son environnement.