Oral du bac: primitive et probabilités
primitive, probabilités (loi binomiale)
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Variations et courbe d'une primitive
- Soit
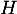 la fonction définie et dérivable sur
la fonction définie et dérivable sur 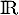 par
par
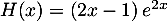 .
.
Démontrer que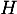 est une primitive sur
est une primitive sur 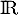 de la fonction
de la fonction 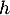 définie par
définie par 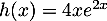 .
.
Existe-t-il d'autres primitives de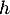 ?
?
- Dresser le tableau de variation de
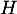 et tracer l'allure de la courbe représentative de
et tracer l'allure de la courbe représentative de 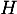 .
.
Correction exercice 1
Cacher la correction
-
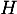 est une primitive de
est une primitive de 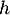 signifie exactement que
signifie exactement que 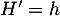 .
Il s'agit donc de calculer la dérivée de
.
Il s'agit donc de calculer la dérivée de 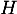 .
.
On dérive un produit,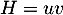 avec
avec 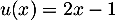 donc
donc 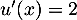 et
et 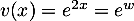 donc
donc 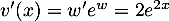 .
.
On obtient alors
![\[H'(x)=u'v+uv'=2e^{2x}+(2x-1)2e^{2x}=4xe^{2x}=h(x)\]](/Generateur-Devoirs/TS/ChapIntegration/exOralPrimitive_c/10.png)
ce qui montre que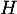 est une primitive de
est une primitive de 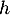 .
.
- Le sens de variation de
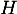 est donné par le signe sa dérivée
est donné par le signe sa dérivée
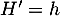 et on peut alors dresser directement le tableau de variation:
et on peut alors dresser directement le tableau de variation:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ &&$0$&& $+\infty$ \\\hline
$4x$ && $-$ &\zb& $+$ &\\\hline
$e^{2x}$ && $+$ &$|$& $+$ &\\\hline
$H'(x)$ && $-$ &\zb& $+$ &\\\hline
&&&&&\\
$H$ && \Large{$\searrow$}&&
\Large{$\nearrow$}&\\
&&&$-1$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/exOralPrimitive_c/15.png)
![\[\psset{xunit=2cm,yunit=1.2cm,arrowsize=8pt}\begin{pspicture*}(-3,-2)(2.2,2.3)
\psline{->}(-3,0)(2,0)
\psline{->}(0,-5)(0,2)
\newcommand{\f}[1]{2 #1 mul -1 add 2.718 #1 2 mul exp mul}
\psplot[linewidth=1pt,linecolor=blue,plotpoints=200]{-5}{3}{\f{x}}
\psline(-.1,-1)(.1,-1)\rput[r](-.1,-1.2){$-1$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exOralPrimitive_c/16.png)
Cacher la correction
Exercice 2: Contrôle qualité pour la production de composants electroniques
Une entreprise fabrique des composants électroniques.
Un contrôle de qualité a établi que la probabilité qu'un composant
soit défectueux à la sortie de la chaîne de production est égale à
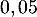 .
.
L'entreprise propose à la vente des lots de 20 composants.
On note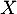 la variable aléatoire égale au nombre de composants
défectueux dans un lot.
la variable aléatoire égale au nombre de composants
défectueux dans un lot.
L'entreprise propose à la vente des lots de 20 composants.
On note
- Quelle est la loi de probabilités suivie par
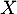 ?
?
- Déterminer la probabilité pour qu'un lot contienne
ne contienne aucun composant défectueux.
- Déterminer la probabilité pour qu'un lot contienne strictement
moins de 10% de composants défectueux.
- Un client souhaite acheter un nombre plus important de
composants et désire donc les acheter par lot de 30.
Déterminer la probabilité pour que dans un tel lot il y ait strictement moins de 10% de composants défectueux.
Correction exercice 2
Cacher la correction
- Pour faire un lot, on répète
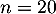 fois l'expérience aléatoire
consistant à tirer au hasard un composant électronique dans la
production.
fois l'expérience aléatoire
consistant à tirer au hasard un composant électronique dans la
production.
Chaque tirage est une épreuve de Bernoulli pour laquelle le succès est de tirer un composant défectueux avec la probabilité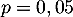 .
.
Ses répétitions sont identiques et indépendantes entre elles.
On en déduit que la variable aléatoire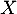 , comptant le nombre de
succès sur ces 20 répétitions, suit la loi binomiale
, comptant le nombre de
succès sur ces 20 répétitions, suit la loi binomiale
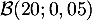 .
.
- L'événement "ne contenir aucun composant défectueux" est
l'événement "
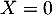 "; sa probabilité est:
"; sa probabilité est:
![\[
P(X=0)
=\lp\begin{array}{c} 20\\0\enar\right) p^0(1-p)^{20-0}
=0,95^{20}\simeq 0,3584\ .
\]](/Generateur-Devoirs/TS/ChapProbabilites/exOralQualite_c/6.png)
La probabilité qu'il n'y ait aucun composant défectueux dans un lot est environ de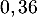 .
.
- 10 % d'objets dans lot correspondent à
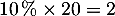 composants défectueux.
La probabilité qu'il y ait strictement moins de 10 % d'objets
défectueux est donc de:
composants défectueux.
La probabilité qu'il y ait strictement moins de 10 % d'objets
défectueux est donc de:
![\[\begin{array}{ll}
P(X<2)
&=P(X=0)+PX(X=1) \\
&\simeq 0,358
+ \lp\begin{array}{c} 20\\1\enar\right) p^1(1-p)^{20-1}\\
&\simeq 0,358+20\tm0,05\tm0,95^{19}
\simeq 0,73
\end{array}
\]](/Generateur-Devoirs/TS/ChapProbabilites/exOralQualite_c/9.png)
La probabilité qu'il y ait astrictement moins de 10 % de composants défectueux est donc d'environ 0,73. - En procédant comme précédemment, avec
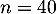 ,
10 % des composants correspondant alors à 3 composants,
,
10 % des composants correspondant alors à 3 composants,
![\[
P(X<3)=P(X=0)+P(X=1)+P(X=2)
\]](/Generateur-Devoirs/TS/ChapProbabilites/exOralQualite_c/11.png)
avec:
![\[\begin{array}{ll}
P(X=0) &= \lp\begin{array}{c} 30\\0\enar\right) p^0(1-p)^{30-0}
=0,95^{30}\simeq 0,21
\\[0.2cm]
P(X=1) &= \lp\begin{array}{c} 30\\1\enar\right) p^1(1-p)^{29}
=30\tm0,05\tm0,95^{29} \simeq 0,34
\\[0.2cm]
P(X=2) &= \lp\begin{array}{c} 30\\2\enar\right) p^2(1-p)^{28}
=435\tm0,05^2\tm0,95^{28} \simeq 0,26
\end{array}
\]](/Generateur-Devoirs/TS/ChapProbabilites/exOralQualite_c/12.png)
La probabilité qu'un lot de composants contiennent strictement moins de 10 % de composants défectueux est donc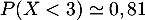 .
.
Cacher la correction
Voir aussi: