Oral du bac: suite, fonction exponentielle

Terminale générale, spécialité mathématiques

L'utilisation d'une calculatrice est autorisée.

La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.

Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.

Exercice 1: Equation du second degré avec exponentielle - Etude du sens de variation

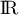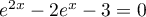Résoudre dans $\R$ l'équation $e^{2x}-2e^x-3=0$ .
(on pourra utiliser le changement de variable )
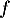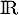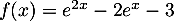Étudier le sens de variation de la fonction définie sur $\R$ par $f(x)=e^{2x}-2e^x-3$ .
Tracer l'allure de sa courbe représentative.

Correction exercice 1

Soit 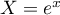, alors 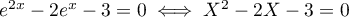. Cette équation du second degré admet deux solutions réelles 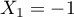et .
On revient ensuite à l'inconnue :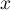
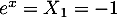- n'a pas de solution, une exponentielle étant toujours strictement positive;
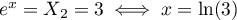- $e^x=X_2=3\iff x=\ln(3)$ .
L'équation a donc comme unique solution rélle .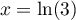
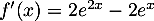On a $f'(x)=2e^{2x}-2e^x$ .
On cherche le signe de cette dérivée, donc à résoudre

$\begin{array}{ll}f'(x)>0\iff 2e^{2x}-2e^x>0 &\iff e^{2x}>e^x\\ &\iff 2x>x\\ &\iff x>0\enar$

et on a donc

$\begin{tabular}{|c|ccccc|}\hline $x$ & $-\infty$ &&$0$&& $+\infty$ \\\hline $f'(x)$ && $-$ &\zb& $+$ &\\\hline &&&&&\\ $g$ && \Large{$\searrow$}&& \Large{$\nearrow$}&\\ &&&$-4$&&\\\hline \end{tabular}$

et la courbe qui va avec (sur laquelle on n'oublie pas de situer la solution trouvée à la question précédente):

$\psset{unit=1cm}\begin{pspicture*}(-5.2,-5.3)(5.2,5.3) \psline{->}(-5.2,0)(5.2,0) \psline{->}(0,-5.3)(0,5.3) \multido{\i=-5+1}{11}{\psline(\i,-.1)(\i,.1)\rput(\i,-.3){\i} \psline(-.1,\i)(.1,\i)\rput[r](-.2,\i){\i} } \psplot{-5}{5}{2.718 x 2 mul exp -2 2.178 x exp mul add -3 add} \end{pspicture*}$

Cacher la correction

Exercice 2: Loi binomiale à la fête foraine

Une attraction dans une fête foraine permet de gagner soit un gros lot, soit une petite peluche.
250 cordelettes sont proposées au joueur, dont 30 sont reliées à un gros lot, et les autres à une petite peluche.
Il est bien sûr impossible pour le joueur de déterminer quelle cordelette est reliée à un gros lot ou à une peluche, et les tirages se font donc au hasard.

Quelle est la probabilité de gagner un gros lot en tirant une cordelette ?
Un joueur achète un ticket lui permettant de tirer 3 cordelettes.
On désigne par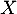 la variable aléatoire égale au nombre de gros lots gagnés par le joueur.
1. Quelle est la loi de probabilité de ?
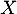2. Déterminer la probabilité de gagner 3 petites peluches.
3. Calculer la probabilité de gagner au moins un gros lot.
4. Quelle est l'espérance de 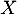? Interpréter ce résultat.

Correction exercice 2

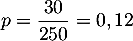Il y a 250 cordelettes, dont 30 sont reliées à un gros lot. La probabilité d'en gagner un est donc $p=\dfrac{30}{250}=0,12$ .
1. Le joueur répète fois l'expérience aléatoire consistant à tirer au hasard une cordelette, pour la quelle la probabilité de succès est .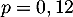
  Ses répétitions sont identiques et indépendantes entre elles.
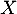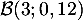  On en déduit que la variable aléatoire , comptant le nombre de succès sur ces 3 répétitions, suit la loi binomiale $\mathcal{B}(3;0,12)$ .
2. L'événement "Gagner 3 petites peluches" est l'événement "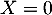", dont la probabilité est donc:
  
  $P(X=0)=\lp\begin{array}{ll} 3 \\ 0\enar\right) \times 0,12^0 \times (1-0,12)^3 \simeq 0,68$
3. L'événement "Gagner au moins un gros lot" est l'événement " 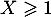$X\geqslant 1$ ", dont la probabilité est donc:
  
  $P(X\geqslant 1)=1-P(X=0)\simeq 1-0,68 = 0,32$
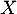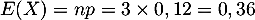4. L'espérance de est: $E(X)=np=3\tm0,12=0,36$ : En effectuant 3 tirages, le joueur peut espérer obtenir en moyenne 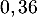gros lot.