Oral de Bac - Fraction rationnelle, décomposition en éléments simples, primitives et intégrale
Exercice corrigé - Spécialité maths, terminale générale
Soit 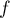 la fonction définie sur
la fonction définie sur ![$I=]1;+\infty[](/Generateur-Devoirs/TS/ChapIntegration/exOral02/2.png) par l'expression
par l'expression
 .
.
- Déterminer trois nombres réels
 ,
,  et
et  tels que,
pour tout
tels que,
pour tout 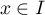 ,
, 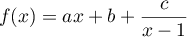 .
.
- En déduire les primitives de
 sur
sur 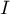 .
.
- Déterminer la primitive
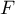 de
de 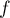 sur
sur 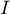 telle que
telle que 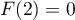 .
.
- Calculer l'intégrale
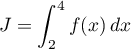 .
.
Correction
Cacher la correction
- En mettant sur le même dénominateur l'expression proposée on a

Ainsi, on cherche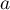 ,
,  et
et 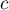 tels que
tels que

On a donc, pour tout ,
, 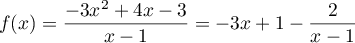
- Les primitives de
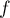 sont de la forme
sont de la forme
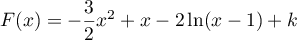 , avec
, avec 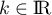 .
.
- Si on impose de plus que
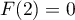 , alors on doit avoir
, alors on doit avoir
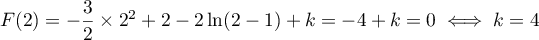 .
.
Ainsi,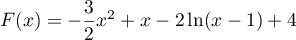 .
.
- Comme
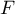 est une primitive de
est une primitive de 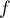 ,
on a
,
on a

Cacher la correction
Tag:Intégrales
Voir aussi:
