Bac 2022 (11 mai): QCM, limite, convexité, primitive
Exercice corrigé - Spécialité maths, terminale générale
Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
- La courbe représentative de la fonction
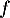 définie sur
définie sur 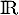 par
par 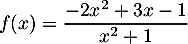 admet pour asymptote
la droite d'équation:
admet pour asymptote
la droite d'équation:
a.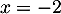
b.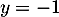
c.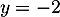
d.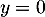
- Soit
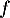 la fonction définie sur
la fonction définie sur 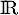 par
par 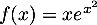 .
.
La primitive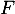 de
de 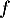 sur
sur 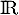 qui vérifie
qui vérifie  est définie par :
est définie par :
a.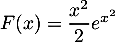
b.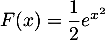
c.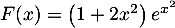 ;
;
d.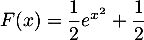
- On donne ci-contre la représentation graphique
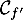 de la fonction dérivée
de la fonction dérivée 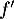 d'une fonction
d'une fonction  définie sur
définie sur 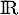 .
.
(10,1)
\psaxes[linewidth=1.25pt,Dx=11,Dy=11](0,0)(-0.5,-5)(10,1)
\psecurve[linewidth=1.25pt,linecolor=blue](-0.3,-6)(-0.2,-5)(0,-4)(1,-1.2)(2,0)(3,0.45)(4,0.5)(5,0.45)(6,0.4)(10,0.1)(11,0.08)
\uput[d](1,0){\footnotesize 1}\uput[d](2,0){\footnotesize 2}\uput[dl](0,0){\footnotesize 0}\uput[d](0,1){\footnotesize 1}
\uput[r](0.4,3.5){$\mathcal{C}_{f'}$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/23.png)
On peut affirmer que la fonction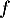 est :
est :
a. concave sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/25.png)
b. convexe sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/26.png)
c. convexe sur [0 ; 2]
d. convexe sur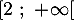
- Parmi les primitives de la fonction
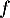 définie sur
définie sur 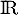 par
par 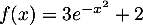 :
:
a. toutes sont croissantes sur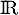
b. toutes sont décroissantes sur
c. certaines sont croissantes sur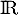 et d'autres
décroissantes sur
et d'autres
décroissantes sur 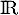
d. toutes sont croissantes sur![$]-\infty~;~0]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/35.png) et
décroissantes sur
et
décroissantes sur 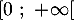
- La limite en
 de la fonction
de la fonction 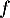 définie sur l'intervalle
définie sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/39.png) par
par 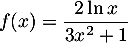 est égale à :
est égale à :
a. ;
;
b.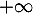 ;
;
c.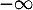
d.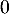
- L'équation
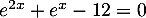 admet dans
admet dans 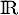 :
:
a. trois solutions;
b. deux solutions;
c. une seule solution;
d. aucune solution.
Correction
Cacher la correction
- c.
On a
![\[\begin{array}{ll}f(x) &= \dfrac{-2x^2 + 3x - 1}{x^2 + 1}\\[1em]
&=\dfrac{-2x^2\lp1-\frac3{2x}+\frac1{2x^2}\right)}{x^2\lp1+\frac1{x^2}\right)}\\[1em]
&=-2\dfrac{1-\frac3{2x}+\frac1{2x^2}}{1+\frac1{x^2}}
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/1.png)
d'où
![\[\lim_{x\to+\infty}f(x)=-2\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/2.png)
et donc la droite d'équation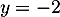 est asymptote.
est asymptote.
- d.
On peut par exemple dériver chacune des propositions, seule la b. et la d. convienne.
Comme on veut de plus que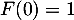 , seule la réponse d. convient finalement.
, seule la réponse d. convient finalement.
- c.
Une fonction est convexe lorsque sa dérivée est croissante (et donc dérivée seconde positive).
Ici on peut conjecturer que la fonction est convexe sur![$]-\infty;3]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/5.png) environ,
et donc en particulier sur
environ,
et donc en particulier sur ![$[0;2]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/6.png) .
.
- a.
Les primitives
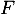 de
de 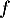 vérifient
vérifient 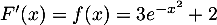 .
En particulier, comme
.
En particulier, comme 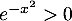 sur
sur 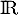 ,
on a
,
on a 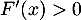 et donc
et donc 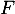 est nécessairement strictement croissante sur
est nécessairement strictement croissante sur 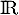 .
.
- d.
On a
![\[f(x) = \dfrac{2\ln x}{3x^2 + 1}
=\dfrac{\ln(x)}{x^2}\tm\dfrac{2}{3+\frac1{x^2}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/15.png)
avec, par croissances comparées
![\[\lim_{x\to+\infty}\dfrac{\ln(x)}{x^2}=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/16.png)
et donc
![\[\lim_{x\to+\infty}f(x)=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/17.png)
- c.
On pose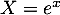 et alors l'équation se réécrit
et alors l'équation se réécrit
![\[X^2+X-12=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/19.png)
c'est une équation du second degré de discriminant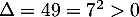 qui admet donc deux solutions réelles distinctes
qui admet donc deux solutions réelles distinctes
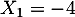 et
et 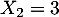 .
.
On revient alors à l'équation de départ:-
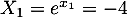 qui est impossible, car
qui est impossible, car 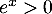 pour tout réel
pour tout réel 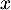
-
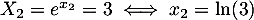
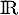 .
.
-
Cacher la correction
Tags:QCMLimites de fonctionsConvexitéPrimitive
Voir aussi:
