Bac 2021 (sujet 0): Arbre pondéré, loi binomiale et python
Exercice corrigé - Spécialité maths, terminale générale
Pour préparer l’examen du permis de conduire, on distingue deux types de formation :
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
On interroge au hasard une personne du groupe considéré.
On considère les évènements suivants :
- la formation avec conduite accompagnée ;
- la formation traditionnelle.
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
- 75 personnes ont suivi une formation avec conduite accompagnée ; parmi elles, 50 ont réussi l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
- 225 personnes se sont présentées à l’examen suite à une formation traditionnelle ; parmi elles, 100 ont réussi l’examen à la première présentation, 75 à la deuxième et 50 à la troisième présentation.
On interroge au hasard une personne du groupe considéré.
On considère les évènements suivants :
-
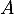 : « la personne a suivi une formation avec conduite accompagnée » ;
: « la personne a suivi une formation avec conduite accompagnée » ;
-
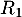 : « la personne a réussi l’examen à la première présentation » ;
: « la personne a réussi l’examen à la première présentation » ;
-
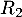 : « la personne a réussi l’examen à la deuxième présentation » ;
: « la personne a réussi l’examen à la deuxième présentation » ;
-
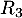 : « la personne a réussi l’examen à la troisième présentation ».
: « la personne a réussi l’examen à la troisième présentation ».
- Modéliser la situation par un arbre pondéré.
Dans les questions suivantes, les probabilités demandées seront données sous forme d’une fraction irréductible.
-
- Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation.
- Montrer que la probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation est égale à
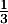 .
.
- La personne interrogée a réussi l’examen à sa deuxième présentation. Quelle est la probabilité qu’elle ait suivi une formation avec conduite accompagnée?
- On note
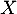 la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
Ainsi,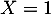 correspond à l’évènement
correspond à l’évènement 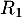 .
.
- Déterminer la loi de probabilité de la variable aléatoire
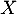 .
.
- Calculer l’espérance de cette variable aléatoire. Interpréter cette valeur dans le contexte de l’exercice.
- Déterminer la loi de probabilité de la variable aléatoire
- On choisit, successivement et de façon indépendante,
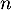 personnes parmi les 300 du groupe étudié, où
personnes parmi les 300 du groupe étudié, où 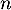 est un entier naturel non nul. On assimile ce choix à un tirage avec remise de
est un entier naturel non nul. On assimile ce choix à un tirage avec remise de 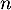 personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l’évènement
personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l’évènement 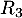 est égale à
est égale à 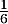 .
.
- Dans le contexte de cette question, préciser un évènement dont la probabilité est égale à
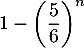 .
On considère la fonction Python seuil ci-dessous, où
.
On considère la fonction Python seuil ci-dessous, où 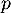 est un nombre réel appartenant à l’intervalle ]0;1[.
est un nombre réel appartenant à l’intervalle ]0;1[.
![\[\begin{tabular}[]{|l|}
\hline
\textbf{def seuil}(p):\\
\hspace{2em}n = 1\\
\hspace{2em}\textbf{while} 1$-$(5/6)**n $< =$ p:\\
\hspace{4.5em}n = n+1\\
\hspace{2em}\textbf{return} n\\
\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0/17.png)
- Quelle est la valeur renvoyée par la commande seuil(0,9) ? Interpréter cette valeur dans le contexte de l’exercice.
- Dans le contexte de cette question, préciser un évènement dont la probabilité est égale à
Correction
Cacher la correction
- On modélise la situation par un arbre pondéré.
{.3}\rput(3.3,1.6){$\frac{25}{75}$}
\rput(4.3,.5){$R_3$}\rput(3.3,.7){$0$}
%
\psline(2.5,-1.5)(4,-1.5)
\psline(4,-.5)(2.5,-1.5)(4,-2.5)
\rput(4.3,-.5){$R_1$}\rput(3.3,-.5){$\frac{100}{225}$}
\rput(4.3,-1.5){$R_2$}\pscircle[linestyle=none,fillstyle=solid,fillcolor=white](3.3,-1.6){.3}\rput(3.3,-1.5){$\frac{75}{225}$}
\rput(4.3,-2.5){$R_3$}\rput(3.3,-2.4){$\frac{50}{225}$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/1.png)
-
- La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation est:
![\[\begin{array}{ll}P\left( A\cap R_2\rp&= P(A)\times P_{A}\left( R_2\rp\\[.3em]
&=\dfrac{75}{300}\tm\dfrac{25}{75}=\dfrac{1}{12}\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/2.png)
- La probabilité que la personne interrogée ait réussi l'examen à sa deuxième présentation est
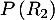 soit, d'après la formule des probabilités totales,
soit, d'après la formule des probabilités totales,
![\[\begin{array}{ll}
P\left( R_2\right) %&= P\left( A\cap R_2\right) + P\left(\overline{A}\cap R_2\right)\\
&= P_A\left( R_2\rp\times P(A) + P_{\overline{A}}\left( R_2\rp\times P\left(\overline{A}\rp\\[.3em]
&=\dfrac{75}{300}\tm\dfrac{25}{75}
+\dfrac{225}{300}\tm\dfrac{75}{225}\\[.7em]
&=\dfrac{25}{300} + \dfrac{75}{300}
=\dfrac{100}{300}=\dfrac13\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/4.png)
- La personne interrogée a réussi l'examen à sa deuxième présentation. La probabilité qu'elle ait suivi une formation avec conduite accompagnée est alors la probabilité conditionnelle:
![\[P_{R_2}(A) = \dfrac{P\left (A\cap R_2 \right )}{P\left (R_2\right )}= \dfrac{\frac{1}{12}}{\frac{1}{3}} = \dfrac{3}{12}=\dfrac{1}{4}
\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/5.png)
- La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation est:
- On note
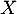 la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s'est présentée à l'examen jusqu'à sa réussite.
la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s'est présentée à l'examen jusqu'à sa réussite.
- La loi de probabilité de la variable aléatoire
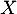 est:
est:
![\[\begin{tabular}{|*4{c|}}
\hline
$x_i$ & 1 & 2 & 3\\
\hline
$p_i=P(X=x_i)$ & $P(R_1)$ & $P(R_2)$ & $P(R_3)$ \\
\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/8.png)
soit, en calculant les différentes probabilités:
Donc la loi de probabilité de la variable aléatoire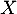 est:
est:
![\[\begin{tabular}{|*4{c|}}
\hline
$x_i$ & 1 & 2 & 3\\
\hline
$p_i=P(X=x_i)$ & $\dfrac{1}{2}$ & $\dfrac{1}{3}$ & $\dfrac{1}{6}$\rule[-10pt]{0pt}{28pt} \\
\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/13.png)
-
- L'espérance de cette variable aléatoire est:
![\[\begin{array}{ll}E(X)&=\dsp\sum_{i=1}^3 x_i\times p_i\\&= 1\times\dfrac{1}{2} + 2 \times \dfrac{1}{3} + 3\times \dfrac{1}{6} \\
&= \dfrac{5}{3}\approx 1,67\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/14.png)
Cela signifie que le nombre de passages pour réussir l'examen est en moyenne de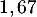 .
.
- La loi de probabilité de la variable aléatoire
- On choisit, successivement et de façon indépendante,
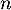 personnes parmi les 300 du groupe étudié, où
personnes parmi les 300 du groupe étudié, où 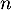 est un entier naturel non nul. On assimile ce choix à un tirage avec remise de
est un entier naturel non nul. On assimile ce choix à un tirage avec remise de 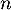 personnes parmi les 300 personnes du groupe.
personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l'évènement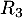 est égale à
est égale à 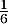 .
.
- On cherche un évènement dont la probabilité est égale à
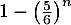 .
.
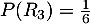 donc
donc 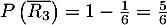 .
Le nombre
.
Le nombre 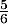 est donc la probabilité de l'événement "
est donc la probabilité de l'événement "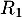 ou
ou 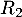 ", c'est-à-dire la probabilité qu'une personne prise au hasard réussisse l'examen à la première tentative ou à la deuxième.
", c'est-à-dire la probabilité qu'une personne prise au hasard réussisse l'examen à la première tentative ou à la deuxième.
La probabilité que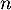 personnes réussissent l'examen à la première ou à la deuxième tentative est de
personnes réussissent l'examen à la première ou à la deuxième tentative est de 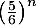 .
.
L'événement de probabilité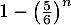 est l'événement contraire du précédent, donc correspond à l'événement "au moins une personne n'a pas réussi l'examen à la première ou à la deuxième tentative", c'est-à-dire "au moins une personne a réussi l'examen à la troisième tentative''.
est l'événement contraire du précédent, donc correspond à l'événement "au moins une personne n'a pas réussi l'examen à la première ou à la deuxième tentative", c'est-à-dire "au moins une personne a réussi l'examen à la troisième tentative''.
- La valeur renvoyée par seuil(0.9) est la première valeur de
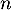 pour laquelle
pour laquelle 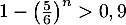 .
.
On résout cette inéquation:
![\[\begin{array}{ll}1-\lp\dfrac56\rp^n >0,9
&\iff
\lp\dfrac56\rp^n<0,1 \\[1em]
&\iff
\ln\lp\lp\dfrac56\rp^n\rp<\ln(0,1)\\[1em]
&\iff
n\ln\lp\dfrac56\rp<\ln(0,1)\\[1em]
&\iff
n<\dfrac{\ln(0,1)}{\ln\lp\dfrac56\right)}\sim12,6
\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/32.png)
La commande seuil(0.9) renvoie donc la valeur 13.
Il faut donc prendre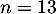 personnes sur les 300 pour que la probabilité d'en avoir une qui a réussi l'examen à sa troisième tentative soit supérieure à
personnes sur les 300 pour que la probabilité d'en avoir une qui a réussi l'examen à sa troisième tentative soit supérieure à 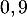 .
.
- On cherche un évènement dont la probabilité est égale à
Cacher la correction
Tag:Probabilités
Voir aussi:
