Bac 2016 (Centres étrangers) : Loi binomiale, arbre
Exercice corrigé - Spécialité maths, terminale générale
Un institut effectue un sondage pour connaître, dans une population donnée, la proportion de personnes qui sont favorables à un projet d'aménagement du territoire. Pour cela, on interroge un échantillon aléatoire de personnes de cette population, et l'on pose une question à chaque personne.
Les deux parties sont relatives à cette même situation, mais peuvent être traitées de manière indépendante.
Partie A : Nombre de personnes qui acceptent de répondre au sondage
On admet dans cette partie que la probabilité qu'une personne interrogée accepte de répondre à la question est égale à 0,6.
Partie B : Correction due à l'insincérité de certaines réponses
Dans cette partie, on suppose que, parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu'elles sont favorables au projet.
L'institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d'entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable. Ainsi, une personne qui se dit favorable peut :
Par expérience, l'institut estime à 15% le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l'opinion de la personne interrogée.
Le but de cette partie est, à partir de ces données, de déterminer le taux réel de personnes favorables au projet, à l'aide d'un modèle probabiliste. On prélève au hasard la fiche d'une personne ayant répondu, et on définit :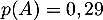
.
Correction
Les deux parties sont relatives à cette même situation, mais peuvent être traitées de manière indépendante.
Partie A : Nombre de personnes qui acceptent de répondre au sondage
On admet dans cette partie que la probabilité qu'une personne interrogée accepte de répondre à la question est égale à 0,6.
- L'institut de sondage interroge 700 personnes. On note
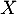la variable aléatoire correspondant au nombre de personnes interrogées qui acceptent de répondre à la question posée.
- Quelle est la loi de la variable aléatoire
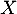? Justifier la réponse.
- Quelle est la meilleure approximation de
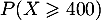parmi les nombres suivants ?
![\[0,92\hspace{2cm} 0,93\hspace{2cm}0,94\hspace{2cm}0,95.\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2016-CE/4.png)
- Quelle est la loi de la variable aléatoire
- Combien de personnes l'institut doit-il interroger au minimum pour garantir, avec une probabilité supérieure à 0,9, que le nombre de personnes répondant au sondage soit supérieur ou égal à 400.
Partie B : Correction due à l'insincérité de certaines réponses
Dans cette partie, on suppose que, parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu'elles sont favorables au projet.
L'institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d'entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable. Ainsi, une personne qui se dit favorable peut :
- soit être en réalité favorable au projet si elle est sincère.
- soit être en réalité défavorable au projet si elle n'est pas sincère.
Par expérience, l'institut estime à 15% le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l'opinion de la personne interrogée.
Le but de cette partie est, à partir de ces données, de déterminer le taux réel de personnes favorables au projet, à l'aide d'un modèle probabiliste. On prélève au hasard la fiche d'une personne ayant répondu, et on définit :
-
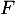l'évènement « la personne est en réalité favorable au projet» ;
-
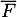l'évènement « la personne est en réalité défavorable au projet» ;
-
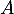l'évènement « la personne affirme qu'elle est favorable au projet»;
-
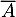l'évènement « la personne affirme qu'elle est défavorable au projet».
.
- En interprétant les données de l'énoncé, indiquer les valeurs de
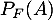et 
.
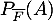- On pose
.
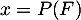- Reproduire sur la copie et compléter l'arbre de probabilité ci-contre.
- En déduire une égalité vérifiée par
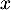
![\[\psset{xunit=1.4cm,yunit=0.5cm}
\begin{pspicture}(2,-3)(3,10)
\psline(1.5,-1.5)(0,0)(1.5,1.5)\rput(1.75,1.5){$F$}\rput(0.8,1.2){$x$}
\rput(1.75,-1.5){$\overline{F}$}\rput(0.8,-1.4){$1-x$}
\psline(3.5,0.5)(2,1.5)(3.5,3.)\rput(3.75,3){$A$}
\rput(3.75,0.5){$\overline{A}$}
\psline(3.5,-0.5)(2,-1.5)(3.5,-3.)\rput(3.75,-3){$\overline{A}$}
\rput(3.75,-0.5){$A$}
\end{pspicture} \]](/Generateur-Devoirs/TS/ChapProbabilites/ex2016-CE/14.png)
- Reproduire sur la copie et compléter l'arbre de probabilité ci-contre.
- Déterminer, parmi les personnes ayant répondu au sondage, la proportion de celles qui sont réellement favorables au projet.
Correction
Tag:Probabilités
Autres sujets au hasard:
Voir aussi: