Exercice bac corrigé - Probabilités: Bac S, métropole, juin 2015
Lois exponentielle et normale - Fluctuation
Exercice corrigé de mathématiques: Exercice bac corrigé - Probabilités: Bac S métropole, juin 2015, Lois exponentielle et normale - Fluctuation
Exercice - énoncé:
Les résultats des probabilités seront arrondis à
Partie 1
- Soit
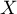 une variable aléatoire qui suit la loi exponentielle de paramètre
une variable aléatoire qui suit la loi exponentielle de paramètre 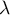 , où
, où 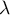 est un réel strictement positif donné.
est un réel strictement positif donné.
On rappelle que la densité de probabilité de cette loi est la fonction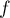 définie sur
définie sur
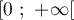 par
par 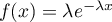 .
.
- Soit
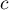 et
et 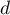 deux réels tels que
deux réels tels que 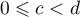 .
Démontrer que la probabilité
.
Démontrer que la probabilité 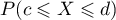 vérifie
vérifie
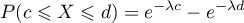
- Déterminer une valeur de
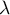 à
à 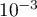 près de telle sorte que la probabilité
près de telle sorte que la probabilité 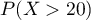 soit égale à 0,05.
soit égale à 0,05.
- Donner l'espérance de la variable aléatoire
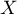 .
.
Dans la suite de l'exercice on prend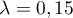 .
.
- Calculer
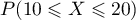 .
.
- Calculer la probabilité de l'évènement
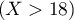 .
.
- Soit
- Soit
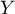 une variable aléatoire qui suit la loi normale d'espérance
une variable aléatoire qui suit la loi normale d'espérance 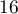 et d'écart type
et d'écart type 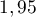 .
.
- Calculer la probabilité de l'événement
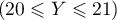 .
.
- Calculer la probabilité de l'événement
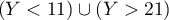 .
.
- Calculer la probabilité de l'événement
Partie 2
Une chaîne de magasins souhaite fidéliser ses clients en offrant des bons d'achat à ses clients privilégiés. Chacun d'eux reçoit un bon d'achat de couleur verte ou rouge sur lequel est inscrit un montant. Les bons d'achats sont distribués de façon à avoir, dans chaque magasin, un quart de bons rouges et trois quarts de bons verts.
Les bons d'achat verts prennent la valeur de
De façon analogue, les bons d'achat rouges prennent les valeurs
- Calculer la probabilité d'avoir un bon d'achat d'une valeur supérieure ou égale à
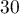 euros sachant qu'il est rouge.
euros sachant qu'il est rouge.
- Montrer qu'une valeur approchée à
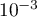 près de la probabilité d'avoir un bon d'achat d'une valeur supérieure ou égale à
près de la probabilité d'avoir un bon d'achat d'une valeur supérieure ou égale à 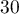 euros vaut
euros vaut 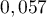 .
.
Pour la question suivante, on utilise cette valeur.
- Dans un des magasins de cette chaîne, sur
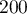 clients
privilégiés,
clients
privilégiés, 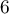 ont reçu un bon d'achat d'une valeur supérieure ou
égale à
ont reçu un bon d'achat d'une valeur supérieure ou
égale à 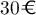 .
.
Le directeur du magasin considéré estime que ce nombre est insuffisant et doute de la répartition au hasard des bons d'achats dans les différents magasins de la chaîne.
Ses doutes sont-ils justifiés ?
Correction exercice
Partie 1
-
- Par définition,
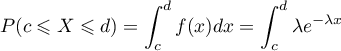 .
.
Or,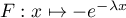 est une primitive de
est une primitive de  et donc,
et donc,
![\[\begin{array}{ll} P(c\leqslant X\leqslant d)&=\dsp\int_c^df(x)dx\\[1em]
&=\Bigl[F(x)\Bigr]_c^d=F(d)-F(c)\\[.8em]
&=-e^{-\lambda d}-\lp-e^{-\lambda c}\rp\\
&=e^{-\lambda c}-e^{-\lambda d}\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/4.png)
- On a
![\[\begin{array}{ll} P(X>20)&=P(0\leqslant X\leqslant 20)\\
&=e^{-\lambda\tm0}-e^{-\lambda\tm20}=1-e^{-20\lambda}\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/5.png)
Ainsi,
![\[\begin{array}{ll} P(X>20)=0,95&\iff 1-e^{-20\lambda}=0,95\\[.8em]
&\iff\lambda=-\dfrac{\ln(0,05)}{20}\simeq 0,150\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/6.png)
- L'espérance d'une loi exponentielle est
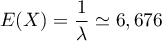 .
.
Dans la suite de l'exercice on prend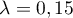 .
.
-
![\[\begin{array}{ll} P(10 \leqslant X \leqslant 20)&=e^{-10\lambda}-e^{-20\lambda}\\
&\simeq 0,173\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/9.png)
-
![\[\begin{array}{ll} P(X>18)&=1-P(0\leqslant X\leqslant 18)\\
&=1-\left( e^{-0\lambda}-e^{-18\lambda}\rp\\
&=e^{-18\lambda}\simeq 0,067\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/10.png)
- Par définition,
-
- La calculatrice donne
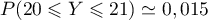 .
.
-
![\[\begin{array}{ll} P((Y < 11) \cup (Y > 21))&=1-P(11\leqslant Y\leqslant 21)\\
&\simeq0,010\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/12.png)
- La calculatrice donne
Partie 2 On peut alors représenter la situation par un arbre, en notant les événements:
- R: "le bon d'achat est rouge"
- V: "le bon d'achat est vert"
- T: "le bon d'achat est de trente euros"
- C: "le bon d'achat est de cent euros"
- A: "le bon d'achat est d'une autre valeur"
![\[\psset{xunit=1.2cm,yunit=1cm}\begin{pspicture}(-.2,-2.8)(4,2.2)
\psline(1.5,-1.5)(0,0)(1.5,1.5)\rput(1.75,1.5){V}
\rput(0.4,0.9){$0,75$}\rput(0.4,-0.9){$0,25$}
\psline(3.5,1)(2,1.5)(3.5,2)\rput(1.75,-1.5){R}
\rput(3.75,2){T}\rput(3.75,1.){A}
\rput(2.8,2.){$0,067$}\rput(2.8,.9){$0,933$}
\psline(2,-1.5)(3.5,-.5)\rput(3.75,-.5){T}
\psline(2,-1.5)(3.5,-1.5)\rput(3.75,-1.5){C}
\psline(2,-1.5)(3.5,-2.5)\rput(3.75,-2.5){A}
\rput(2.8,-0.7){$0,015$}\rput(2.95,-1.35){$0,010$}\rput(2.8,-2.5){$0,975$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/13.png)
- En notant S l'événement: "la valeur du bon d'achat est
supérieure ou égale à 30 euros", la probabilité recherchée est la
probabilité conditionnelle:
![\[P_R(S)=P_R(T)+P_R(C)=0,025\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/14.png)
-
![\[\begin{array}{ll} P(S) &= P(T\cup C)\\[.8em]
&=P(V)\times P_V(S)+P(R)\times P_R(S)\\[.8em]
&=0,75\tm0,067+0,025\tm0,025=0,0565\simeq 0,057\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/15.png)
- En utilisant la valeur précédente, la probabilité d'avoir un bon d'un montant supérieur ou égal à 30 euros est
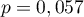 .
.
Comme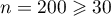 ;
; 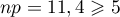 et
et
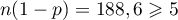 , on peut utiliser la formule asymptotique de
l'intervalle de fluctuation à 95%:
la proportion
, on peut utiliser la formule asymptotique de
l'intervalle de fluctuation à 95%:
la proportion 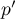 dans un échantillon aléatoire de 200 bons d'achat
est, avec une probabilité d'environ 95%, dans l'intervalle de fluctuation
dans un échantillon aléatoire de 200 bons d'achat
est, avec une probabilité d'environ 95%, dans l'intervalle de fluctuation
![\[\begin{array}{ll} I&=\left[p-1,96\tm\dfrac{\sqrt{p(1-p)}}{\sqrt{n}}~;~p+1,96\tm\dfrac{\sqrt{p(1-p)}}{\sqrt{n}}\right]\\&\simeq \Bigl[0,024;0,090\Bigr]\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2015-Metropole-Juin_c/21.png)
Ici, la proportion observée est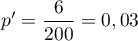 .
On a
.
On a 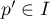 , et donc les doutes du directeur du magasin ne sont pas
justifiés: avec un faible risque d'erreur (d'environ 5%), la
fluctuation de
, et donc les doutes du directeur du magasin ne sont pas
justifiés: avec un faible risque d'erreur (d'environ 5%), la
fluctuation de  par rapport à celle de
par rapport à celle de  annoncée s'explique
simplement par le fait que l'échantillon des 200 billets de son
magasin est constitué au hasard.
annoncée s'explique
simplement par le fait que l'échantillon des 200 billets de son
magasin est constitué au hasard.
Cacher la correction
Voir aussi: