Exercice bac corrigé - Probabilités: Bac S, Amérique du sud 2013
Base de donnée de la sécurité sociale
Exercice corrigé de mathématiques: Exercice corrigé - Probabilités: Bac S Amérique du sud 2013 - Utilisation de la base de donnée de la sécurité sociale
Exercice - énoncé:
Dans cet exercice, les résultats seront arrondis à 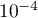 près.
près.
Partie A
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%. L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :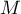 : « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
: « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
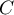 : « La personne est victime d'un accident cardiaque au cours de sa vie ».
: « La personne est victime d'un accident cardiaque au cours de sa vie ».
Partie B
La sécurité sociale décide de lancer une enquête de santé publique, sur ce problème de malformation cardiaque de type anévrisme, sur un échantillon de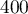 personnes, prises au hasard dans la population française.
On note
personnes, prises au hasard dans la population française.
On note 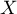 la variable aléatoire comptabilisant le nombre de personnes de l'échantillon présentant une malformation cardiaque de type anévrisme.
la variable aléatoire comptabilisant le nombre de personnes de l'échantillon présentant une malformation cardiaque de type anévrisme.
Partie C
Partie A
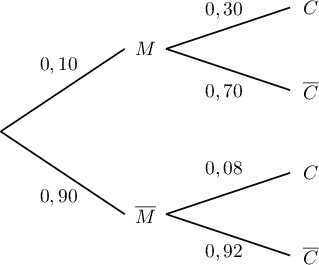
On peut construire l'arbre pondéré suivant:
Partie B
Partie C
Cacher la correction
Partie A
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%. L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :
-
- Montrer que
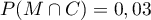 .
.
- Calculer
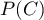 .
.
- Montrer que
- On choisit au hasard une victime d'un accident cardiaque. Quelle est la probabilité qu'elle présente une malformation cardiaque de type anévrisme ?
Partie B
La sécurité sociale décide de lancer une enquête de santé publique, sur ce problème de malformation cardiaque de type anévrisme, sur un échantillon de
- Définir la loi de la variable aléatoire
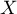 .
.
- Déterminer
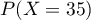 .
.
- Déterminer la probabilité que
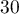 personnes de ce groupe, au moins, présentent une malformation cardiaque de type anévrisme.
personnes de ce groupe, au moins, présentent une malformation cardiaque de type anévrisme.
Partie C
- On considère la variable aléatoire
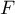 , définie par
, définie par 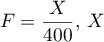 étant la variable aléatoire de
la partie B.
Déterminer l'intervalle de fluctuation asymptotique de la variable aléatoire
étant la variable aléatoire de
la partie B.
Déterminer l'intervalle de fluctuation asymptotique de la variable aléatoire 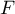 au seuil de
au seuil de 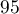 %.
%.
- Dans l'échantillon considéré,
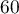 personnes présentent une malformation cardiaque de type anévrisme.
Qu'en pensez-vous ?
personnes présentent une malformation cardiaque de type anévrisme.
Qu'en pensez-vous ?
Correction exercice
Partie A
On peut construire l'arbre pondéré suivant:

-
-
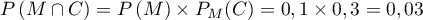
- En utilisant l'arbre (ou d'après la formule des probabilités totales):
![\begin{array}{ll}
P(C)&=P\left( M \cap C\right) + P\left(\overline M \cap C\right)\\[0.3cm]
&= P(M)\times P_M(C) + P\lp\overline M\rp\times P_{\overline M}(C) \\[0.3cm]
&= 0,1\times 0,3 + 0,9 \times 0,08 = 0,03 + 0,072 = 0,102\enar](/Generateur-Devoirs/TS/ChapProbabilites/ex113.AmeriqueSud_c/3.png)
-
- On choisit au hasard une victime d'un accident cardiaque.
La probabilité qu'elle présente une malformation cardiaque de type anévrisme est
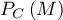 :
:
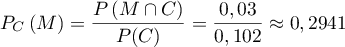
Partie B
- On peut considérer que, choisir au hasard un échantillon de 400 personnes, peut être assimilé à un tirage avec remise de 400 personnes dans la population totale.
Or la probabilité qu'une personne souffre d'une malformation cardiaque de type anévrisme est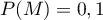 d'après l'énoncé.
d'après l'énoncé.
Donc on peut dire que la variable aléatoire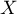 qui donne le nombre de personnes souffrant de cette malformation cardiaque suit une loi binomiale de paramètres
qui donne le nombre de personnes souffrant de cette malformation cardiaque suit une loi binomiale de paramètres 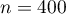 et
et 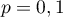 .
.
- Comme
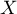 suit la loi binomiale
suit la loi binomiale 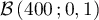 ,
,
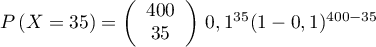 ;
;
le résultat donné par la calculatrice est approximativement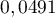 .
.
- La probabilité que
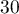 personnes de ce groupe, au moins,
présentent une malformation cardiaque de type anévrisme est
personnes de ce groupe, au moins,
présentent une malformation cardiaque de type anévrisme est
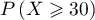 qui est égale à
qui est égale à 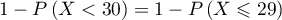 .
.
D'après la calculatrice,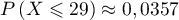 ,
donc
,
donc 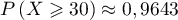 .
.
Partie C
- On sait que si
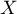 suit la loi binomiale
suit la loi binomiale 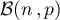 , alors l'intervalle de fluctuation asymptotique de la variable aléatoire
, alors l'intervalle de fluctuation asymptotique de la variable aléatoire 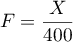 au seuil de
au seuil de 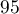 % est donné par:
% est donné par:
![\begin{array}{ll}
I&=\left[ p-1,96\dfrac{\sqrt{p(1-p)}}{\sqrt n}\,;\,p+1,96\dfrac{\sqrt{p(1-p)}}{\sqrt n}\rb\\[0.6cm]
&=\left[ 0,1-1,96\dfrac{\sqrt{0,1(1-0,1)}}{\sqrt{400}}\,;\,0,1+1,96\dfrac{\sqrt{0,1(1-0,1)}}{\sqrt{400}}\rb\\[0.6cm]
&=\Bigl[ 0,0706\,;\, 0,1294\Bigr]
\enar](/Generateur-Devoirs/TS/ChapProbabilites/ex113.AmeriqueSud_c/23.png)
- Dans l'échantillon considéré,
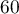 personnes présentent une malformation cardiaque de type anévrisme;
personnes présentent une malformation cardiaque de type anévrisme; 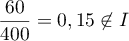 .
Le taux de malades dans cet échantillon est anormalement élevé.
.
Le taux de malades dans cet échantillon est anormalement élevé.
Cacher la correction
Voir aussi: