Exercice corrigé type bac - Etude complète de fonction
Une étude complète de fonction
Exercice corrigé de mathématiques: Un exercice corrigé complet type Bac: Etude complète de fonctions, variations, limites, asymptote oblique...
Exercice - énoncé:
Partie I. Soit
- Etudier le sens de variation de
 sur
sur  .
.
- Démontrer que l'équation
 admet dans
admet dans  une
solution unique que l'on notera
une
solution unique que l'on notera  .
Donner une valeur approchée de
.
Donner une valeur approchée de  à
à  près.
près.
- Déterminer le signe de
 sur
sur  .
.
Partie II. Soit
- Etudier les limites de
 aux bornes de ses intervalles de
définition.
aux bornes de ses intervalles de
définition.
En déduire l'existence de deux asymptotes verticales dont on donnera les équations. - Calculer la dérivée de
 sur
sur  et
déterminer son signe.
et
déterminer son signe.
- Dresser le tableau de variation de
 .
.
- Montrer que pour tout
 de
de  ,
,
 .
.
- Montrer que la droite
 d'équation
d'équation  est une
asymptote oblique à
est une
asymptote oblique à  en
en  et
et  .
.
- Etudier la position relative de
 et
et  .
.
- Déterminer les abscisses des points de
 admettant une tangente parallèle à
admettant une tangente parallèle à  .
.
Correction exercice
Partie I.
-
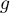 est une fonction polynôme donc dérivable sur
est une fonction polynôme donc dérivable sur 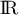 ,
et, pour tout
,
et, pour tout 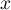 réel,
réel,
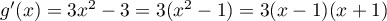 .
.
-
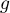 est une fonction polynôme, donc continue sur
est une fonction polynôme, donc continue sur  .
De plus, sa limite en
.
De plus, sa limite en 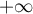 est la limite de son terme de plus
haut degré:
est la limite de son terme de plus
haut degré:  ,
et comme
,
et comme 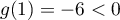 , on en déduit, d'après le théorème des valeurs
intermédiaires, que il existe un unique réel
, on en déduit, d'après le théorème des valeurs
intermédiaires, que il existe un unique réel ![$\alpha\in]1;+\infty[](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/14.png) tel que
tel que 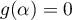 .
Comme de plus,
.
Comme de plus, 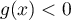 pour tout
pour tout ![$x\in]-\infty;1]](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/17.png) , on en déduit
que
, on en déduit
que
![$\alpha\in]1;+\infty[](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/18.png) est la seule solution sur
est la seule solution sur 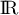 de
l'équation
de
l'équation  .
.
De plus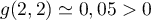 et
et 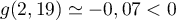 ,
donc
,
donc 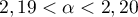 .
.
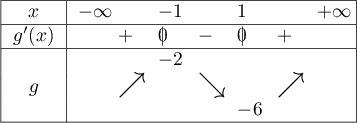
- On déduit de la question précédcente le signe de
 :
:
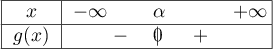
Partie II. Soit
- Limites en
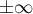 :
:
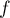 est une fonction rationnelle, et on peut donc factoriser par ses
termes de plus haut degré au numérateur et dénominateur (termes
prépondérants en l'infini):
est une fonction rationnelle, et on peut donc factoriser par ses
termes de plus haut degré au numérateur et dénominateur (termes
prépondérants en l'infini):
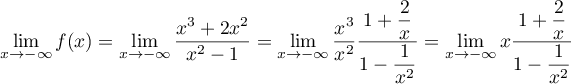
On a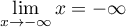 et
et
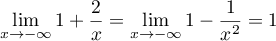 ,
et donc, par quotient et produit des limites,
,
et donc, par quotient et produit des limites,
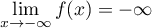 .
.
De même, en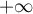 ,
,
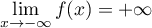 .
.
Limites en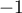 :
Signe de
:
Signe de 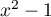 :
:
![[c]{|c|*6{p{0.3cm}}p{0.5cm}|}\hline
$x$ & $-\infty$ && $-1$ && $1$ && $+\infty$ \\\hline
$x^2-1$ && $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \\\hline](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/40.png)
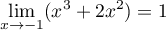 et
et
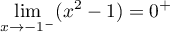 ,
d'où,
,
d'où,  .
.
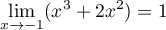 et
et
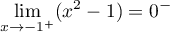 ,
d'où,
,
d'où, 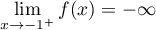 .
.
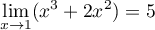 et
et
 ,
d'où,
,
d'où, 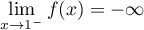 .
.
 et
et
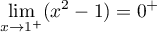 ,
d'où,
,
d'où, 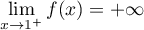 .
.
On en déduit que les droites d'équation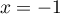 et
et 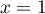 sont
asymptotes verticales à
sont
asymptotes verticales à 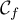 .
.
-
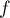 est le quotient des fonctions polynômes
est le quotient des fonctions polynômes
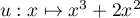 et
et 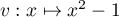 qui sont dérivables sur
qui sont dérivables sur
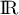 , avec
, avec 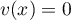 si et seulement si
si et seulement si 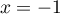 ou
ou 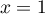 , et donc,
, et donc,
 est dérivable sur
est dérivable sur 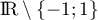 ,
avec, pour tout
,
avec, pour tout 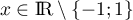 ,
,
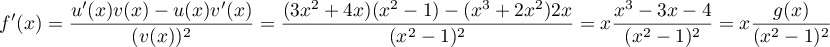
- On en déduit, d'après la partie I,
(0,0.9)
\psline[linewidth=0.2pt](0.1,-0.7)(0.1,0.9)& \Large{$\nearrow$}
&& \Large{$\searrow$}
&\psline[linewidth=0.2pt](0,-0.7)(0,0.9)
\psline[linewidth=0.2pt](0.1,-0.7)(0.1,0.9)& \Large{$\searrow$}
&& \Large{$\nearrow$}
&\\
&$\scriptstyle-\infty$&&$\ \scriptstyle-\infty$&&&$\ \ \scriptstyle-\infty$&&&$\scriptstyle f(\alpha)$&&\\\hline](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/67.png)
- Pour tout
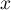 de
de 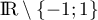 ,
,
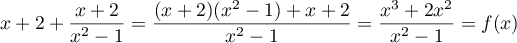 .
.
Ainsi, pour tout de
de 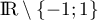 ,
,
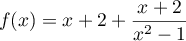 .
.
- D'après le calcul précédent, pour tout
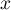 de
de
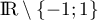 ,
, 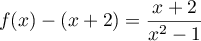 .
.
Ainsi,![$\dsp\lim_{x\to-\infty}\big[f(x)-(x+2)\big]
=\lim_{x\to-\infty}\frac{x+2}{x^2-1}
=\lim_{x\to-\infty}\frac{1}{x}\,\frac{1+\frac{2}{x}}{1-\frac{1}{x^2}}=0](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/77.png)
par produit et quotient des limites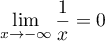 , et
, et
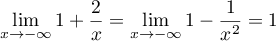 .
.
et de même,![$\dsp\lim_{x\to+\infty}\big[f(x)-(x+2)\big]=0](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/80.png) .
.
Ainsi, la droite est asymptote oblique à
est asymptote oblique à
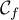 en
en  et
et 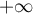 .
.
- La position relative de
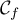 et
et 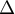 est donnée par le
signe de
est donnée par le
signe de 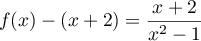 :
:

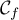 est au-dessous de
est au-dessous de  pour
pour
![$x\in]-\infty;-2]\cup]-1;1[](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/91.png) .
.
 est au dessus de
est au dessus de 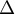 pour
pour
![$x\in[-2;-1[\cup]1;+\infty[](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/94.png) .
.
- Le coefficient directeur de
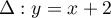 est
est 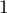 .
Le coefficient de la tangente à
.
Le coefficient de la tangente à 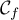 au point d'abscisse
au point d'abscisse  est
est
 .
.
La tangente à au point d'abscisse
au point d'abscisse 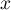 est donc parallèle à
est donc parallèle à
 si et seulement si,
si et seulement si,
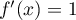 , soit pour
, soit pour 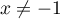 et
et  ,
,
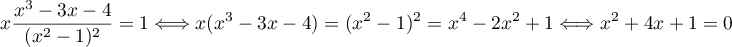
Ce trinôme du second degré a pour discriminant ,
et admet donc deux racines réelles distinctes:
,
et admet donc deux racines réelles distinctes:
 et
et 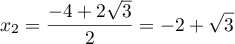
Les abscisses des points de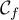 admettant une
tangente parallèle à
admettant une
tangente parallèle à  sont donc:
sont donc:
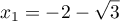 et
et  .
.
![\psset{xunit=1.2cm,yunit=0.9cm}
\begin{pspicture}(-5,-4)(8,9.5)
\psline[linewidth=0.5pt]{->}(-5,0)(5,0)\rput(-0.2,0.25){$O$}
\psline[linewidth=0.5pt]{->}(0,-5)(0,8.5)
\psplot[linewidth=1.2pt]{-5}{-1.058}{
x x mul x mul 2 x mul x mul add
x x mul 1 sub div}
\psplot[linewidth=1.4pt]{-0.908}{0.8}{
x x mul x mul 2 x mul x mul add
x x mul 1 sub div}
\psplot[linewidth=1.4pt]{1.25}{6}{
x x mul x mul 2 x mul x mul add
x x mul 1 sub div}
\rput(1.6,8){$\mathcal{C}_f$}
\psline[linewidth=0.5pt](-1,-5)(-1,9)
\psline[linewidth=0.5pt](1,-5)(1,9)
\psplot[linewidth=0.5pt]{-5}{6}{x 2 add}% Delta
\rput(6,7.6){$\Delta$}
\psline[linewidth=0.5pt]{<->}(1.2,5.29)(3.2,5.29)%Tgte horizontale en 0
\psline[linewidth=0.9pt]{<->}(-0.8,0)(0.8,0)%Tgte horizontale en alpha
\psline[linewidth=0.3pt,linestyle=dashed](2.2,0)(2.2,5.29)
\rput(2.2,-0.2){$\alpha$}
\rput(-1.2,-0.2){$\scriptstyle -1$}
\rput(1.2,-0.2){$\scriptstyle -1$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapFonctions/ex02_c/114.png)
Cacher la correction
Voir aussi: