Exercice corrigé type bac - Etude d'une fonction
Ajustement des paramètres d&pos;une fonction et son étude
Exercice corrigé de mathématiques: Un exercice corrigé complet type Bac: Ajustement des paramètres d'une fonction, puis son étude complète
Exercice - énoncé:
D'après sujet de bac
Partie A
Soit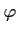 la fonction numérique de la variable réelle
la fonction numérique de la variable réelle 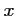 telle
que:
telle
que:
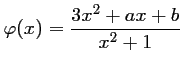 .
.
Déterminer les réels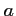 et
et  pour que la courbe représentative de
pour que la courbe représentative de
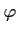 soit tangente au point
soit tangente au point 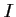 de coordonnées
de coordonnées 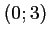 à la droite
à la droite
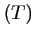 d'équation
d'équation 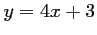 .
.
Partie B
Soit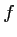 la fonction numérique de la variable réelle
la fonction numérique de la variable réelle 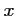 telle que:
telle que:
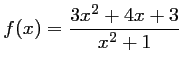 .
.
Partie A La courbe représentative de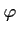 passe par
passe par 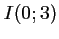 ,
donc
,
donc
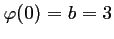 .
.
Cacher la correction
Partie A
Soit
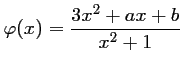 .
.
Déterminer les réels
Partie B
Soit
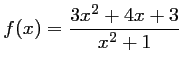 .
.
- Montrer que pour tout
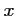 réel,
réel,
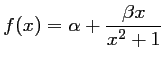 ,
,
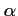 et
et  étant deux réels que l'on déterminera.
étant deux réels que l'on déterminera.
- Etudier la fonction
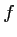 .
.
- Etudier la position de la courbe
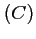 représentative de
représentative de 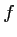 par
rapport à la tangente
par
rapport à la tangente 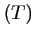 au point
au point 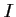 de coordonnées
de coordonnées 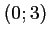 .
.
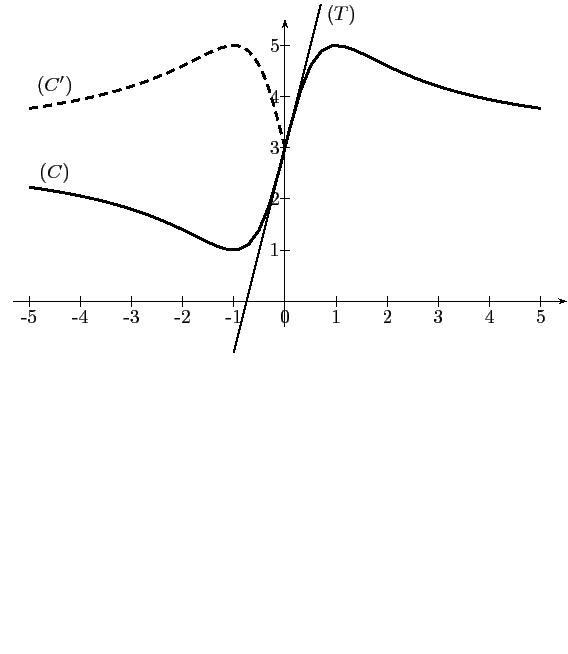
- Construire la courbe
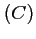 ;
on prendre pou unité 2 cm.
;
on prendre pou unité 2 cm.
- Soit
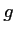 la fonction numérique de la variable réelle
la fonction numérique de la variable réelle 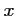 telle
que:
telle
que:
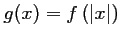 et
et 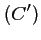 sa courbe représentative.
Sans étudier la fonction
sa courbe représentative.
Sans étudier la fonction 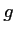 , construire
, construire  sur le graphique
précédent.
sur le graphique
précédent.
Correction exercice
Partie A La courbe représentative de
Le coefficient directeur de la tangente ![]() est
est
![]() .
.
De plus, pour tout réel ![]() ,
,
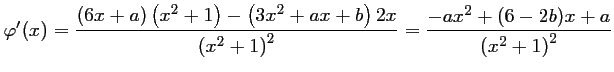 ,
et donc,
,
et donc,
![]() .
On en déduit donc que
.
On en déduit donc que ![]() .
.
Partie B
- Pour tout réel
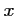 ,
,
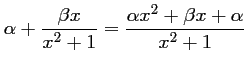
Ainsi,
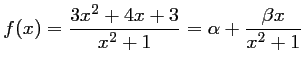 pour
pour 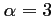 et
et 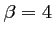 , et on a donc,
, et on a donc,
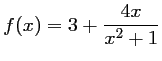 .
.
- En utilisant l'expression précédente on a,
pour tout réel
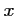 ,
,
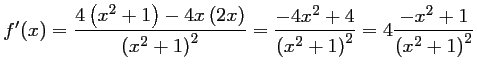 et donc, comme pour tout
et donc, comme pour tout 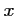 réel,
réel,
 ,
,
arrowsize=5pt 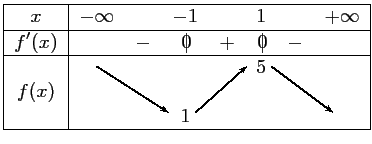
- Pour tout réel
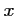 ,
,
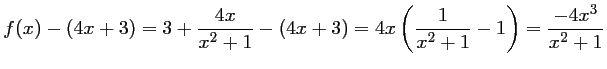 .
.
Ainsi, comme pour tout réel
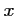 ,
, 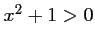 ,
si
,
si 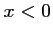 ,
,
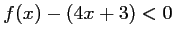 et
et
 est au-dessous de
est au-dessous de 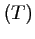 ,
tandis que
si
,
tandis que
si  ,
,
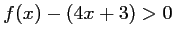 et
et
 est au-dessus de
est au-dessus de 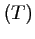 .
.
- 5.
Cacher la correction
Voir aussi: