Exercice corrigé type bac - Nombres complexes
Polynôme complexe et géométrie dans le plan complexe
Exercice corrigé de mathématiques: Exercice corrigé type Bac: Nombres complexes, polynôme et géométrie dans le plan complexe
Exercice - énoncé:
On considère le polynôme  défini par:
;
défini par:
;
 .
.
On considère le polynôme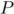 défini par:
;
défini par:
;
 .
.
Cacher la correction
 défini par:
;
défini par:
;
 .
.
- Calculer
 et
et  ,
puis trouver un polynôme
,
puis trouver un polynôme  du second degré à coefficients réels
tel que, pour tout
du second degré à coefficients réels
tel que, pour tout  ,
on ait
,
on ait  .
.
- Résoudre dans
 l'équation
l'équation  .
.
- Placer dans le plan complexe rapporté au repère orthonormal
 les points
les points  ,
,  ,
,  et
et  d'affixes
respectives
d'affixes
respectives
 ,
,  ,
,
 et
et  ,
puis montrer que ces quatre points appartiennent à un même cercle.
,
puis montrer que ces quatre points appartiennent à un même cercle.
- On note
 le symétrique de
le symétrique de  par rapport à
par rapport à  .
.
Conjecturer la nature du triangle ,
puis démontrer votre conjecture.
,
puis démontrer votre conjecture.
Correction exercice
On considère le polynôme
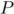 défini par:
;
défini par:
;
 .
.
-
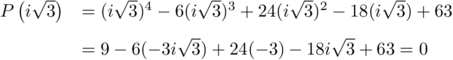
Pour tout complexe , on a:
, on a:
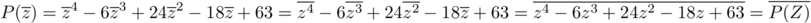
et donc, pour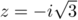 ,
,
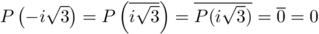 .
.
Le polynôme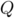 recherché est au plus du second degré, et s'écrit
donc sous la forme
recherché est au plus du second degré, et s'écrit
donc sous la forme
 , où
, où  ,
,  et
et 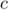 sont trois nombres réels.
sont trois nombres réels.
On a donc,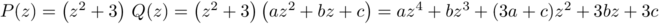
et on doit donc avoir: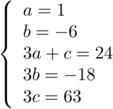 ,
soit
,
soit 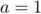 ,
, 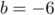 , et
, et 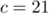 .
.
Ainsi,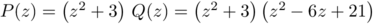 .
.
-
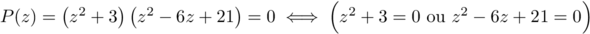 .
.
La première équation a pour solutions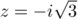 et
et
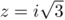 .
.
La deuxième équation a pour discriminant ,
et admet donc deux solutions complexes conjuguées:
,
et admet donc deux solutions complexes conjuguées:
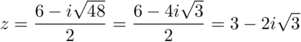 et
et 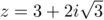 .
.
L'équation admet donc quatre solutions: .
.
-
A l'aide de la représentation dans le plan complexe,
on peut conjecturer que ces quatre points appartiennent au cercle de
centre
 d'affixe
d'affixe 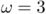 .
.
On vérifie cette conjecture: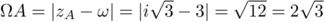 ,
,
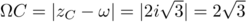 ,
puis, par symétrie,
,
puis, par symétrie,
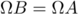 , et
, et 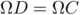 .
.
Ainsi, , et les quatre points
appartiennent bien au même cercle.
, et les quatre points
appartiennent bien au même cercle.
-
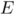 a pour affixe
a pour affixe 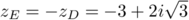 .
Le triangle
.
Le triangle 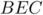 est isocèle, par symétrie.
De plus,
est isocèle, par symétrie.
De plus,
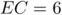 ,
, 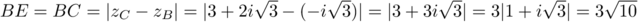 .
.
Ainsi, le triangle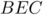 est isocèle,
mais n'est pas équilatéral, ni rectangle (d'après le théorème de
Pythagore, car
est isocèle,
mais n'est pas équilatéral, ni rectangle (d'après le théorème de
Pythagore, car 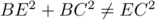 ).
).
Cacher la correction
Voir aussi: