Exercice corrigé bac S - Nouvelle Calédonie 2012 - Nombres complexes
Racines d'un polynôme du 3ème degré - Géométrie dans le plan complexe
Exercice corrigé de mathématiques: Exercice corrigé Bac S, Nouvelle Calédonie 2012: Nombres complexes, racines d'un polynôme du 3ème degré et géométrie dans le plan complexe
Exercice - énoncé:
Partie A. On considère le polynôme 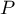 défini sur
défini sur  par
par
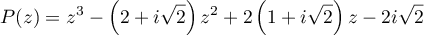
Partie B. Le plan complexe est muni d'un repère orthonormé direct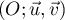 . On prendra 2 cm pour unité graphique.
On considère les points
. On prendra 2 cm pour unité graphique.
On considère les points 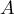 ,
, 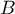 ,
, 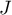 et
et 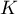 d'affixes respectives:
d'affixes respectives:

Nouvelle Calédonie, 2012 5 points
Partie A.
Partie B.
Cacher la correction
- Montrer que le nombre complexe
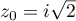 est solution de l'équation
est solution de l'équation 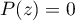 .
.
-
- Déterminer les réels
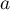 et
et  tels que
tels que 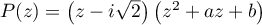 .
.
- En déduire les solutions dans
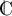 de l'équation
de l'équation 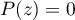 .
.
- Déterminer les réels
Partie B. Le plan complexe est muni d'un repère orthonormé direct
- Placer les points
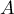 ,
, 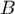 ,
, 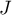 ,
, 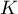 sur une figure qui sera complétée au fur et à mesure de l'exercice.
sur une figure qui sera complétée au fur et à mesure de l'exercice.
- Soit
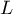 le symétrique du point
le symétrique du point 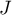 par rapport au point
par rapport au point 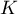 . Montrer que l'affixe de L est égale à
. Montrer que l'affixe de L est égale à 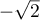 .
.
- Montrer que les points
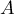 ,
, 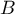 ,
, 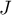 et
et 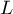 appartiennent à un même cercle dont on précisera le centre et le rayon.
appartiennent à un même cercle dont on précisera le centre et le rayon.
- Soit
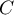 et
et 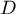 les points d'affixes respectives
les points d'affixes respectives
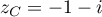 et
et 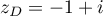 .
.
Quelle est la nature du quadrilatère ABCD ? Justifier la réponse.
Correction exercice
Nouvelle Calédonie, 2012 5 points
Partie A.
-
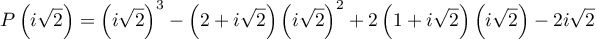
avec,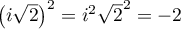 ,
et
,
et 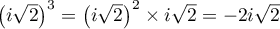 et ainsi,
et ainsi,
![\begin{array}{ll}P\left( i\sqrt2\right)
&=-2i\sqrt2+2\lp2+i\sqrt2\rp+2\lp1+i\sqrt2\rp\lp i\sqrt2\rp-2i\sqrt2\\[0.3cm]
&=-2i\sqrt2+4+2i\sqrt2+2i\sqrt2-4-2i\sqrt2
=0\enar](/Generateur-Devoirs/TS/ChapComplexes/ex112.NC_c/4.png)
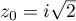 est donc bien une racine de
est donc bien une racine de  .
.
-
- En développant, on a:
![\begin{array}{ll}\left( z-i\sqrt2\rp\left( z^2+az+b\rp
&=z^3+az^2+bz-z^2i\sqrt2-azi\sqrt2-bi\sqrt2\\[0.3cm]
&=z^3+\left( a-i\sqrt2\right) z^2+\left( b-ai\sqrt2\right) z-bi\sqrt2\enar](/Generateur-Devoirs/TS/ChapComplexes/ex112.NC_c/7.png)
En identifiant avec les coefficients du polynôme , on a alors:
, on a alors:
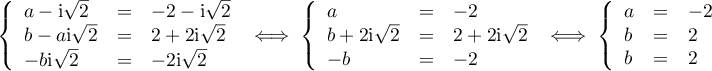
On a donc la factorisation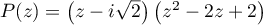
- En utilisant la factorisation précédente :
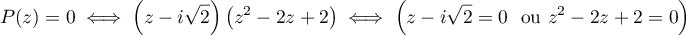
On retrouve la racine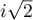 de la question 1.
de la question 1.
L'équation du second degré a pour discriminant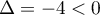 , et
admet donc 2 racines complexes conjuguées:
, et
admet donc 2 racines complexes conjuguées:
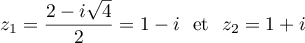
Les solutions sont donc :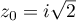 ,
, 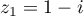 , et
, et 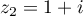 .
.
- En développant, on a:
Partie B.
-
![\psset{unit=2cm,arrowsize=7pt}
\begin{pspicture}(-2,-2)(2,2)
%\psgrid[gridlabels=0pt,subgriddiv=1,gridcolor=orange,gridwidth=0.2pt]
\multido{\i=-2+1}{5}{
\psline[linewidth=0.3pt,linestyle=dashed](\i,-2.2)(\i,2.2)
\psline[linewidth=0.3pt,linestyle=dashed](-2.2,\i)(2.2,\i) }
\psline[linewidth=1.6pt]{->}(-2.2,0)(2.4,0)
\psline[linewidth=1.6pt]{->}(0,-2.2)(0,2.4)
\psdots(1,1)(1,-1)(0,1.414)(1;135)(-1,-1)(-1,1)(-1.414,0)
\uput[ur](1,1){A}\uput[dr](1,-1){B}\uput[l](0,1.414){J}\uput[ul](1;135){K}
\uput[ul](-1,1){D}\uput[d](-1.414,0){L}\uput[dl](-1,-1){C}\uput[dl](0,0){O}
\pspolygon(1,1)(1,-1)(-1,-1)(-1,1)
\end{pspicture}](/Generateur-Devoirs/TS/ChapComplexes/ex112.NC_c/18.png)
- On a
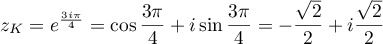 .
.
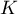 est le milieu du segment
est le milieu du segment ![$[JL]](/Generateur-Devoirs/TS/ChapComplexes/ex112.NC_c/21.png) ce qui se traduit par:
ce qui se traduit par:
![\left\{\begin{array}{l c l}
x_K &=& \dfrac12\left( x_J+x_L\rp\\[0.3cm]
y_K &=& \dfrac12\left( y_J+y_L\right)
\end{array}\right. \iff \left\{\begin{array}{lcl}
-\dfrac{\sqrt2}{2}&=&\dfrac12\lp0 + x_L\rp\\[0.3cm]
\dfrac{\sqrt2}{2}&=&\dfrac12\lp\sqrt2+y_L\right)
\end{array}\right. \iff \left\{\begin{array}{l c l}
x_L&=&- \sqrt{2}\\[0.3cm]
y_L&=&0
\end{array}\right.](/Generateur-Devoirs/TS/ChapComplexes/ex112.NC_c/22.png)
On a donc bien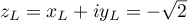 .
.
- On a
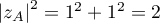 ,
,
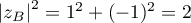 ,
,
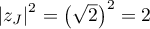
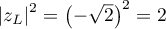 .
.
On a donc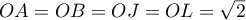 : les points
: les points 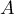 ,
, 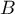 ,
, 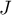 et
et 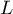 appartiennent à un même cercle de centre
appartiennent à un même cercle de centre 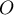 et de rayon
et de rayon 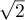 .
.
-
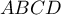 est un carré; on peut raisonner pour le démontrer de
nombreuses manières: en calculant les longueurs
est un carré; on peut raisonner pour le démontrer de
nombreuses manières: en calculant les longueurs 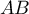 ,
, 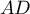 et
et 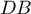 et en utilisant le théorème de Pythagore; en montrant que
et en utilisant le théorème de Pythagore; en montrant que
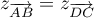 donc que
donc que 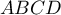 est un parallélogramme, et
en calculant le produit scalaire (avec les coordonnées cartésiennes)
est un parallélogramme, et
en calculant le produit scalaire (avec les coordonnées cartésiennes)
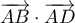 ; ou encore en utilisant le point
; ou encore en utilisant le point  ,
intersection et milieu des diagonales…
,
intersection et milieu des diagonales…
Par exemple,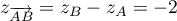 et
et 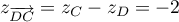 ,
d'où
,
d'où
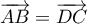 et le quadrilatère
et le quadrilatère  est donc un
parallélogramme.
est donc un
parallélogramme.
De plus,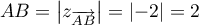 ,
et
,
et 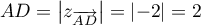 ,
et
,
et 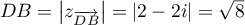 .
.
Ainsi,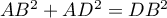 donc, d'après le théorème de Pythagore,
le parallélogramme
donc, d'après le théorème de Pythagore,
le parallélogramme 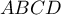 est un rectangle, et comme de plus
est un rectangle, et comme de plus
 , c'est un carré.
, c'est un carré.
Cacher la correction
Voir aussi: