Exercice corrigé bac STI2D / STL - Métropole juin 2014 - Fonction exponentielle et équation différentielle du 1er ordre
Exponentielle et équation différentielle du 1er ordre
Exercice corrigé de mathématiques: Exercice corrigé du bac STI2D / STL - Métropole juin 2014 - Fonction exponentielle et équation différentielle du 1er ordre
Exercice - énoncé:
Dans cet exercice, la température est exprimée en degrés Celsius
(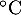 ) et le temps
) et le temps 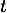 est exprimé en heures.
est exprimé en heures.
Une entreprise congèle des ailerons de poulet dans un tunnel de congélation avant de les conditionner en sachets. À l'instant , les ailerons, à une température de
, les ailerons, à une température de 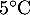 ,
sont placés dans le tunnel.
Pour pouvoir respecter la chaîne du froid, le cahier des
charges impose que les ailerons aient une température inférieure ou
égale à
,
sont placés dans le tunnel.
Pour pouvoir respecter la chaîne du froid, le cahier des
charges impose que les ailerons aient une température inférieure ou
égale à 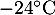 .
.
Partie A
La température des ailerons dans le tunnel de congélation est modélisée en fonction du temps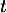 par la fonction
par la fonction 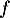 définie sur
l'intervalle
définie sur
l'intervalle 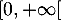 par
par 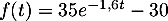 .
.
Partie B
Pour moderniser son matériel, l'entreprise a investi dans un nouveau tunnel de congélation.
La température des ailerons dans ce nouveau tunnel est modélisée, en fonction du temps, par une fonction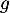 définie et dérivable sur
l'intervalle
définie et dérivable sur
l'intervalle 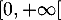 , qui est solution de l'équation
différentielle
, qui est solution de l'équation
différentielle 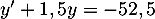
Partie A
Partie B
Pour moderniser son matériel, l'entreprise a investi dans un nouveau tunnel de congélation.
La température des ailerons dans ce nouveau tunnel est modélisée, en fonction du temps, par une fonction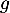 définie et dérivable sur
l'intervalle
définie et dérivable sur
l'intervalle 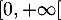 , qui est solution de l'équation
différentielle
, qui est solution de l'équation
différentielle 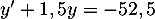
Cacher la correction
Une entreprise congèle des ailerons de poulet dans un tunnel de congélation avant de les conditionner en sachets. À l'instant
Partie A
La température des ailerons dans le tunnel de congélation est modélisée en fonction du temps
- Déterminer la température atteinte par les ailerons au bout de 30 minutes, soit 0,5 h.
- Étudier le sens de variation de la fonction
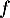 .
.
- Si les ailerons de poulet sont laissés une heure et demie dans le tunnel de congélation, la température des ailerons sera-t-elle conforme au cahier des charges ?
- Résoudre par le calcul l'équation
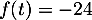 et interpréter le
résultat trouvé.
et interpréter le
résultat trouvé.
Partie B
Pour moderniser son matériel, l'entreprise a investi dans un nouveau tunnel de congélation.
La température des ailerons dans ce nouveau tunnel est modélisée, en fonction du temps, par une fonction
- Résoudre l'équation différentielle
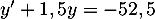 .
.
-
- Justifier que
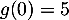 .
.
- Vérifier que la fonction
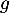 est définie par
est définie par 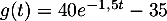 .
.
- Justifier que
- Ce nouveau tunnel permet-il une congélation plus rapide ?
Correction exercice
Partie A
- La température atteinte au bout de
30 minutes est
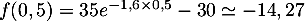 .
.
- On a
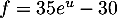 ,
avec
,
avec 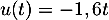 donc
donc 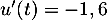 ,
,
et alors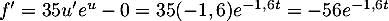 .
.
Comme, pour tout réel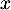 ,
, 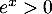 , on a
, on a
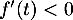 pour tout
pour tout 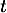 , et donc
, et donc 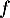 est décroissante sur
l'intervalle
est décroissante sur
l'intervalle 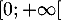 .
.
- Après une heure et demie dans le tunnel de congélation,
la température des ailerons sera de
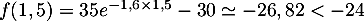 et sera donc conforme au cahier des charges.
et sera donc conforme au cahier des charges.
-
![\[\begin{array}{lll}
f(t)=-24&\iff 35e^{-1,6t}-30=-24
&\iff e^{-1,6t}=\dfrac{-24+30}{35}=\dfrac{6}{35}\\[1em]
&\iff -1,6t=\ln\lp\dfrac{6}{35}\right)
&\iff t=-\dfrac{1}{1,6}\ln\lp\dfrac{6}{35}\rp\simeq 1,10
\enar\]](/Generateur-Devoirs/TSTI/EquaDiff/ex2014-Metropole_c/13.png)
Il faut donc environ 1,10 heure, soit environ une heure et 6 minutes pour que la température des ailerons soit conforme au cahier des charges.
Partie B
Pour moderniser son matériel, l'entreprise a investi dans un nouveau tunnel de congélation.
La température des ailerons dans ce nouveau tunnel est modélisée, en fonction du temps, par une fonction
- L'équation différentielle sans second membre
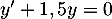 a pour solution générale
a pour solution générale
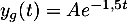 , pour tout réel
, pour tout réel 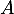 .
.
Une solution particulière de l'équation différentielle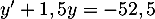 est
est 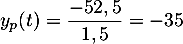 .
.
Ainsi, les solutions de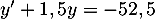 sont
sont
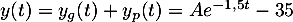 ,
,
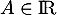 .
.
-
-
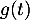 est la température des ailerons dans le tunnel de
congélation au bout d'un temps
est la température des ailerons dans le tunnel de
congélation au bout d'un temps 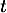 .
À l'entrée du tunnel, soit à
.
À l'entrée du tunnel, soit à  ,
la température est de
,
la température est de 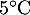 ,
en d'autres termes
,
en d'autres termes 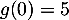 .
.
-
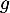 est une solution de l'équation différentielle précédente,
donc
est une solution de l'équation différentielle précédente,
donc 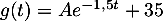 ;
de plus,
;
de plus, 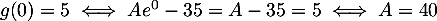 .
.
Ainsi, on a bien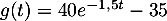 .
.
-
- De même qu'à la question 4. de la partie A,
on a
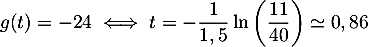
La congélation s'effectue maintenant en environ 0,86 heure, soit environ 51 minutes, et est donc plus rapide.
Cacher la correction
Voir aussi: