Exercice corrigé: Calcul avec vecteurs et coordonnées
Calcul vectoriel - Colinéarité, alignement et intersection de droites
Seconde générale
Exercice corrigé de mathématiques: Exercice corrigé: Vecteurs, coordonnées et géométrie - Points d'une droite, colinarité de vecteurs - Intersection de deux droites
Exercice - énoncé:
On considère, dans un repère  du plan,
les points
du plan,
les points
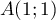 ,
,  ,
, 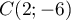 et
et  .
.
Cacher la correction
- Le point
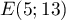 appartient-il à
appartient-il à 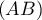 ?
?
- Le point
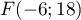 appartient-il à
appartient-il à 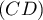 ?
?
- Déterminer les coordonnées du point
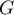 de
de 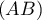 et d'ordonnée 9.
et d'ordonnée 9.
- Déterminer les coordonnées du point
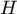 de
de 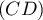 et d'abscisse
et d'abscisse 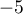 .
.
-
- Montrer que les droites
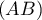 et
et 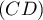 sont sécantes.
sont sécantes.
- Déterminer les coordonnées du point
 d'intersection
de
d'intersection
de 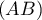 et
et 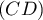 .
.
- Montrer que les droites
Correction exercice
-
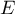 appartient à
appartient à 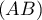 si et seulement si
si et seulement si 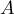 ,
, 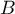 et
et 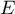 sont alignés, donc si et seulement si
sont alignés, donc si et seulement si 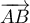 et
et 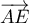 sont
colinéaires, ce qui est le cas car
on a
sont
colinéaires, ce qui est le cas car
on a 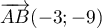 et
et 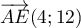 , et
, et
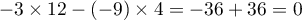 .
.
- De même,
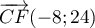 et
et 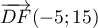 , et
, et
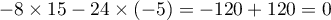 , donc
, donc
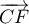 et
et 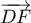 sont colinéaires et alors
sont colinéaires et alors
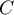 ,
, 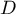 ef
ef 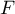 sont lignés, ou encore
sont lignés, ou encore 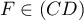 .
.
-
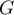 a comme ordonnée 9, donc soit
a comme ordonnée 9, donc soit 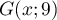 .
De même que précédemment,
on a
.
De même que précédemment,
on a 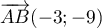 et
et 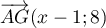 ,
et donc
,
et donc
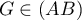 si et seulement si
si et seulement si 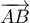 et
et 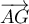 colinéaires,
si et seulement si
colinéaires,
si et seulement si
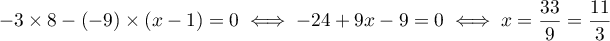 .
.
-
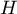 a comme abscisse
a comme abscisse 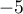 , donc soit
, donc soit 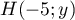 .
On a
.
On a 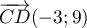 et
et 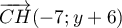 et donc
et donc
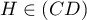 si et seulement si
si et seulement si 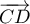 et
et 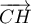 colinéaires
soit
colinéaires
soit
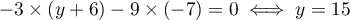 .
.
-
- Les vecteurs
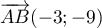 et
et 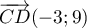 ne sont pas
colinéaires, car
ne sont pas
colinéaires, car 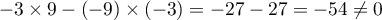 ,
et donc les droites
,
et donc les droites 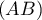 et
et 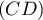 ne sont pas parallèles,
donc sécantes.
ne sont pas parallèles,
donc sécantes.
- Soit
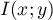 le point d'intersection de
le point d'intersection de 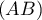 et
et 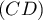 .
.
Alors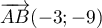 et
et 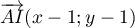 sont colinéaires,
donc
sont colinéaires,
donc 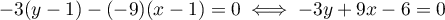 .
.
De même,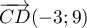 et
et 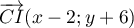 sont colinéaires,
donc
sont colinéaires,
donc 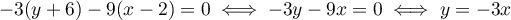 .
.
En reportant dans la première équation, on obtient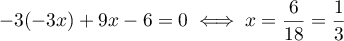 .
.
Enfin, comme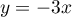 , on a alors
, on a alors 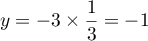 .
.
Ainsi, l'intersection de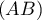 et
et 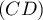 est
est 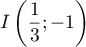 .
.
- Les vecteurs
Cacher la correction
Voir aussi: