Exercice corrigé - Concourance de trois droites contrainte par une hyperbole
Concourance de trois droites
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé: Concourance de trois droites contrainte par une hyperbole
Exercice - énoncé:
Dans un repère orthonormé, on donne les points
 ,
,  et
et  .
.
 est la courbe représentative de la fonction inverse
est la courbe représentative de la fonction inverse
 .
.
Cacher la correction
 .
.
Soit deux réels ![]() et
et ![]() , et
, et ![]() un point quelconque du plan
auquel on associe les points
un point quelconque du plan
auquel on associe les points ![]() et
et ![]() .
.
On souhaite étudier la position relative des droites
![]() ,
, ![]() et
et ![]() .
.
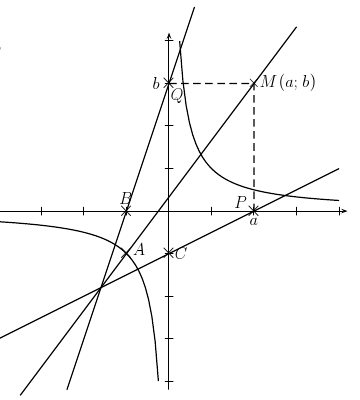
- Placer sur une figure ces six points, représenter la courbe
 et les droites
et les droites
 ,
,  et
et  .
.
- a. Calculer les coordonnées des vecteurs
 ,
,
 et
et
 en fonction de
en fonction de  et
et  .
.
- b. Montrer que ces vecteurs sont colinéaires si et seulement si
 .
.
- c. Que dire alors des droites
 ,
,  et
et  lorsque
lorsque  est un point de
est un point de
 ?
?
- a. Calculer les coordonnées des vecteurs
- On suppose par la suite que
 .
.
- a. Démontrer que la droite
 a pour équation
a pour équation  .
.
- b. Déterminer une équation de la droite
 .
.
- c. Calculer en fonction de
 et
et  les coordonnées du point
les coordonnées du point
 intersection de
intersection de  et
et  .
.
- a. Démontrer que la droite
Correction exercice
-
- a.
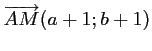 ;
;
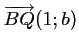 et
et
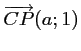 .
.
- b. Les vecteurs
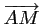 et
et
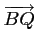 sont colinéaires
si et seulement si:
sont colinéaires
si et seulement si:
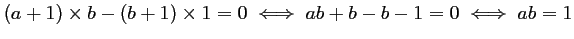
De même, les vecteurs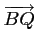 et
et
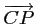 sont colinéaires si et
seulement si:
sont colinéaires si et
seulement si:
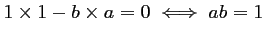
Finalement, ces tois vecteurs sont colinéaires si et seulement si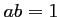 .
.
- c.
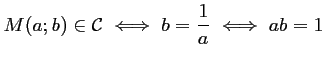 .
On en déduit donc que lorsque
.
On en déduit donc que lorsque 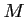 est un point de
est un point de
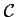 ,
les vecteurs
,
les vecteurs
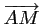 ,
,
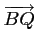 et
et
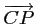 sont colinéaires, et
donc que les droites
sont colinéaires, et
donc que les droites 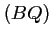 ,
, 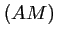 et
et 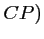 sont parallèles.
sont parallèles.
- a.
- On suppose par la suite que
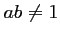 .
.
- a. La droite
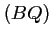 a pour vecteur directeur
a pour vecteur directeur
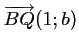 et a donc une équation cartésienne de la forme
et a donc une équation cartésienne de la forme
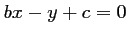 .
De plus
.
De plus
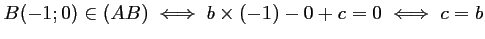
La droite
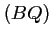 a donc pour équation
a donc pour équation 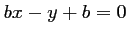 .
.
- b.
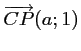 est un vecteur directeur de la droite
est un vecteur directeur de la droite 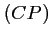 qui a donc une équation cartésienne de la forme
qui a donc une équation cartésienne de la forme
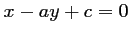 .
.
De plus,
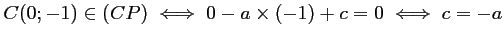 .
.
La droite
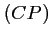 à donc pour équation
à donc pour équation
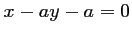 .
.
- c.
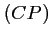 et
et 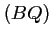 se coupent en
se coupent en 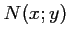 tel que
tel que
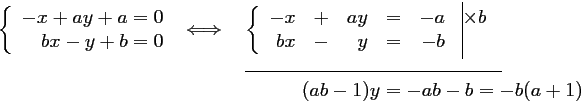
D'où,
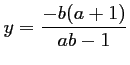 .
.
On alors,
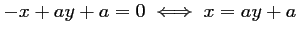 ,
d'où,
,
d'où,
![$\displaystyle x=-a\dfrac{b(a+1)}{ab-1}+a
=a\left[-\dfrac{b(a+1)}{ab-1}+1\right]
=a\left[\dfrac{-b-1}{ab-1}\right]
=\dfrac{-a(b+1)}{ab-1}
$](/Generateur-Devoirs/1S/Chap4/ex3_c_img29.png)
On a donc
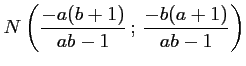 .
.
- a. La droite
Cacher la correction
Voir aussi: