Exercice corrigé - Produit scalaire - Ensemble de points du plan
ROC: théorème de la médiane - Application
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Produit scalaire - Ensemble de points du plan défini par une relation avec un produit scalaire
Exercice - énoncé:
- On note
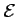 l'ensemble des points
l'ensemble des points 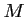 tels que:
tels que:
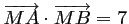 .
.
- a.
- Démontrer que
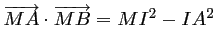 .
.
- b.
- En déduire que
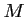 appartient à
appartient à
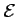 si et seulement
si:
si et seulement
si: 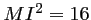 .
.
- c.
- Déterminer alors l'ensemble
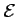 .
.
- On note
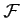 l'ensemble des points
l'ensemble des points 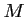 tels que:
tels que:
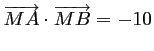 .
Déterminer l'ensemble
.
Déterminer l'ensemble
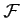 .
.
Correction exercice
- a.
-
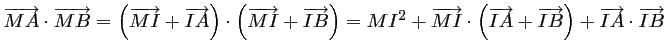
or,
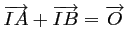 car
car 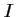 est le milieu de
est le milieu de ![$ [AB]$](/Generateur-Devoirs/1S/Chap6/ex3_c_img4.png) ,
et de même
,
et de même
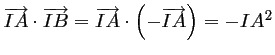 .
.
On a donc bien ainsi,
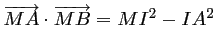 .
.
- b.
- On a alors,
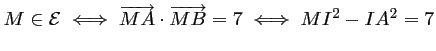 or,
or,
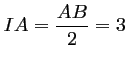 , d'où
, d'où 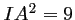 ,
et donc,
,
et donc,
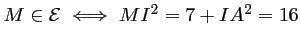 .
.
- c.
-
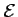 est donc le cercle de centre
est donc le cercle de centre 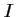 et de rayon
et de rayon
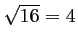 .
.
- En procédant comme précédemment, on a:
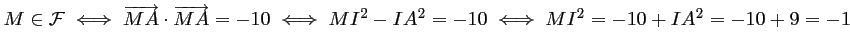 ce qui est impossible car pour tout point
ce qui est impossible car pour tout point 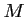 ,
,
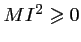 .
.
Ainsi l'ensemble
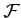 est vide:
est vide:
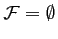 .
.
Cacher la correction
Voir aussi: