Exercice corrigé - Probabilités - Loi binomiale
Contrôle qualité dans une usine de composants électronique
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Probabilités - Répétition d'expériences: loi binomiale - Calcul d'espérance
Exercice - énoncé:
Une entreprise fabrique des composants électroniques.
Un contrôle de qualité a établi que la probabilité qu'un composant
soit défectueux à la sortie de la chaîne de production est égale à
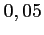 .
.
Cacher la correction
L'entreprise propose à la vente des lots de 20 composants.
On note ![]() la variable aléatoire égale au nombre de composants
défectueux dans un lot.
la variable aléatoire égale au nombre de composants
défectueux dans un lot.
- Montrer que la variable aléatoire
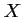 suit une loi binomiale
dont on précisera les paramètres.
suit une loi binomiale
dont on précisera les paramètres.
- Déterminer la probabilité pour qu'un lot contienne
ne contienne aucun composant défectueux.
- Déterminer la probabilité pour qu'un lot contienne strictement
moins de 10% de composants défectueux.
- Un client souhaite acheter un nombre plus important de
composants et désire donc les acheter par lot de 30.
Déterminer la probabilité pour que dans un tel lot il y ait strictement moins de 10% de composants défectueux.
Correction exercice
- Pour faire un lot, on répète
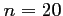 fois l'expérience aléatoire
consistant à tirer au hasard un composant électronique dans la
production.
fois l'expérience aléatoire
consistant à tirer au hasard un composant électronique dans la
production.
Chaque tirage est une épreuve de Bernoulli pour laquelle le succès est de tirer un composant défectueux avec la probabilité
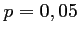 .
.
Ses répétitions sont identiques et indépendantes entre elles.
On en déduit que la variable aléatoire
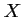 , comptant le nombre de
succès sur ces 20 répétitions, suit la loi binomiale
, comptant le nombre de
succès sur ces 20 répétitions, suit la loi binomiale
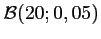 .
.
- L'événement "ne contenir aucun composant défectueux" est
l'événement "
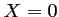 "; sa probabilité est:
"; sa probabilité est:
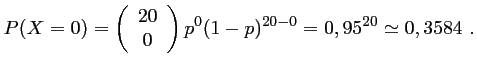
La probabilité qu'il n'y ait aucun composant défectueux dans un lot est environ de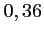 .
.
- 10% d'objets dans lot correspondent à
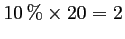 composants défectueux.
composants défectueux.
La probabilité qu'il y ait strictement moins de 10% d'objets défectueux est donc de:
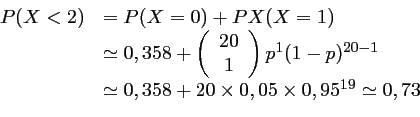
La probabilité qu'il y ait astrictement moins de 10% de composants défectueux est donc d'environ 0,73. - En procédant comme précédemment, avec
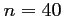 ,
10% des composants correspondant alors à 3 composants,
,
10% des composants correspondant alors à 3 composants,
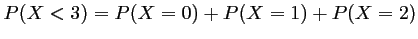
avec: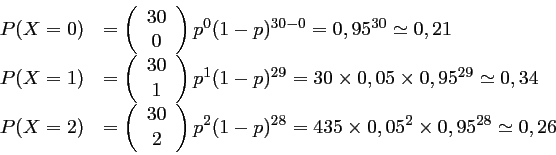
La probabilité qu'un lot de composants contiennent strictement moins de 10% de composants défectueux est donc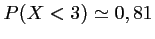 .
.
Cacher la correction
Voir aussi: