Exercice corrigé - Etude d'une fonction avec une racine carrée
Dérivée, sens de variation, encadrements
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Etude d'une fonction avec racine carrée - Dérivée, sens de variation, encadrements
Exercice - énoncé:
On appelle 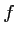 la fonction définie sur
la fonction définie sur
 par
par
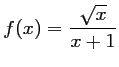 .
.
On appelle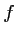 la fonction définie sur
la fonction définie sur
 par
par
 .
.
Cacher la correction
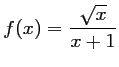 .
.
- Montrer que, pour tout
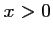 ,
,
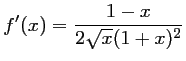 .
.
- Dresser le tableau de variation de
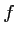 .
.
En déduire que, pour tout réel positif
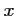 ,
,
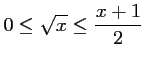 .
.
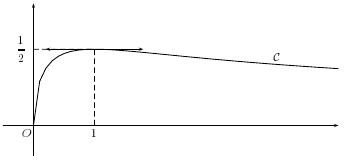
- Tracer la courbe
 de
de 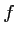 dans le plan muni d'un
repère
dans le plan muni d'un
repère
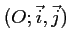 d'unité 2cm en abscisse et 5cm en
ordonnée.
d'unité 2cm en abscisse et 5cm en
ordonnée.
- Montrer que l'équation
 admet une unique
solution
admet une unique
solution 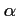 sur
sur ![$ [0;1]$](/Generateur-Devoirs/1S/Chap3/ex9_img12.png) .
.
Donner un encadrement de
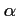 à
à 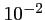 près.
près.
Correction exercice
On appelle
 .
.
- Pour tout
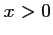 ,
,
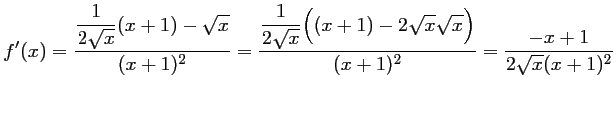
- Pour tout
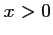 ,
, 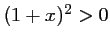 et
et
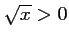 .
Ainsi,
.
Ainsi, 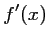 est du signe de
est du signe de 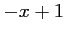 :
:
![$\displaystyle \begin{tabular}[t]{\vert c\vert ccccc\vert}\hline
$x$& $0$\ & & ...
... {$\nearrow$} &
& \Large {$\searrow$} & \\
&0&& && \\ \hline
\end{tabular}$](/Generateur-Devoirs/1S/Chap3/ex9_c_img10.png)
D'après le tableau de variation de
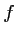 ,
pour tout
,
pour tout
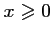 ,
,
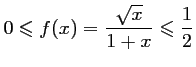 ,
d'où, en mulipliant par
,
d'où, en mulipliant par 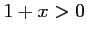 ,
,
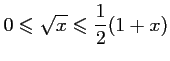 .
.
-
- La fonction
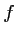 est dérivable sur
est dérivable sur ![$ ]0;1]$](/Generateur-Devoirs/1S/Chap3/ex9_c_img16.png) ,
strictement croissante sur
,
strictement croissante sur ![$ [0;1]$](/Generateur-Devoirs/1S/Chap3/ex9_c_img17.png) avec
avec
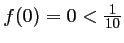 et
et
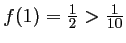 .
.
Ainsi, d'après le théorème des valeurs intermédiaires, il existe un unique réel
![$ \alpha\in[0;1]$](/Generateur-Devoirs/1S/Chap3/ex9_c_img20.png) tel que
tel que
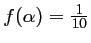 .
.
A l'aide de la calculatrice, on trouve que
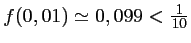 et
et
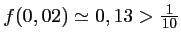 .
.
Ainsi,
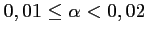 .
.
Cacher la correction
Voir aussi: