Exercice corrigé: Généralités sur une fonction

Vocabulaire et graphique autour d'une fonction


Seconde générale


Exercice corrigé de mathématiques: Exercice corrigé: généralités sur une fonction: images, antécédent, tableau de variation, résolution graphqiue d'équations/inéquation

Exercice - énoncé:

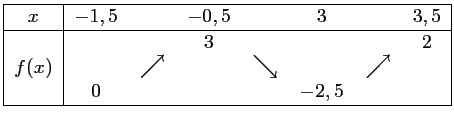
On considère la fonction f dont la représentation graphique est donnée ci-contre.
Les réponses seront données avec la précision permise par le graphique.

1. Déterminer l'ensemble de définition $ D$ de $ f$ .
2. Déterminer les images des nombres $ -1$ et 0 .
3. Déterminer les antécédents de $ -1,5$ et $ 1$ .
4. Dresser le tableau de variations de $ f$ .
5. Résoudre graphiquement l'équation $ f(x)=2$ .
6. Résoudre graphiquement l'équation $ f(x)\leq 0$ .
7. Soit $ g$ la fonction définie sur $ {\rm I\kern-.1567em R}$ par $ g(x)=-x+1$ .

a. Tracer la représentation graphique de la fonction $ g$ .
b. En déduire les solutions de l'équation $ f(x)=-x+1$ .

8. Quelles valeurs de $ m$ peut-on choisir pour qu'il y ait exactement deux solutions à l'équation $ f(x)=m$ ?

\begin{pspicture}(-2.4,-3.5)(5,4.5) \psline[linewidth=0.8pt]{->}(-2.5,0)(4.8,0)... ...1)(2,0)(2.5,-1.5) (2.8,-2.3)(3,-2.5)(3.2,-2)(3.4,0)(3.5,2) \par \end{pspicture}

Correction exercice


1. $ D_f=[-1,5\,;\,3,5]$


2. L'image de $ -1$ est $ f(-1)=2$ ; celle de 0 est $ f(0)=2,5$ .


3. Il y a deux antécédents de $ -1,5$ : $ 2,5$ et environ $ 3,2$ .

Il y trois antécédents de $ 1$ : environ $ -1,2$ ; $ 1$ et $ 3,5$ .


4.

$\displaystyle \begin{tabular}{\vert c\vert ccccccc\vert}\hline $x$\ & $-1,5$\ ... ...earrow$} && \Large {$\nearrow$}&\\ &$0$&&&&$-2,5$&&\\ \hline \end{tabular} $


5. L'équation $ f(x)=2$ admet tois solutions : $ x=-1$ , environ $ x=0,3$ , et $ x=3,5$ .
6. On a $ f(x)\leq 0$ pour $ x\in\left\{-1,5\right\}\cup[2\,;\,3,4]$ .
7.
a. $ g$ est une fonction affine, sa courbe représentative $ \mathcal{C}_g$ est donc une droite.
b. Les solutions de l'équation $ f(x)=-x+1=g(x)$ sont données par les abscisses des points d'intersections des deux courbes, soit $ x=-1$ , $ x=2,5$ et environ $ x=3,1$ .

8. L'équation $ f(x)=m$ admet exactement deux solutions lorsque $ m\in]2\,;\,3[$ ou $ m\in]-2,5\,;\,0[$

\begin{pspicture}(-2.4,-3.5)(5,4.5) \psline[linewidth=0.8pt]{->}(-2.5,0)(4.8,0)... ...pt]{-2.2}{4.1}{-1 x mul 1 add} \rput(-1.7,3.3){$\mathcal{C}_g$} \end{pspicture}


Cacher la correction


Voir aussi:
ccc