Exercice corrigé: Rentabilité et bénéfice maximal d’une usine
Etude de fonction
Seconde générale
Exercice corrigé de mathématiques: Exercice corrigé: Etude de fonction - Etude de la rentabilité et bénéfice maximal d’une usine
Exercice - énoncé:
Monsieur Dupré, PDG d'une société fabriquant du mobilier urbain,
s'intéresse au bénéfice réalisé par sa société.
Il fabrique et vend, par semaine,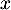 lots de mobilier.
lots de mobilier.
Le coût unitaire de production, en euros,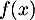 (coût de production
pour un lot de
mobilier) s'exprime en fonction du nombre de lots
(coût de production
pour un lot de
mobilier) s'exprime en fonction du nombre de lots 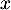 par
l'expression:
par
l'expression:
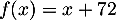 .
.
A ce coût unitaire s'ajoute des frais de fonctionnement de l'usine de production s'élevant à 3 952 euros par semaine, quelle que soit la quantité de lots produite.
Cacher la correction
Il fabrique et vend, par semaine,
Le coût unitaire de production, en euros,
A ce coût unitaire s'ajoute des frais de fonctionnement de l'usine de production s'élevant à 3 952 euros par semaine, quelle que soit la quantité de lots produite.
-
Chaque lot est vendu 200 euros. Montrer que le bénéfice réalisé pour
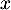 lots produits et vendus est:
lots produits et vendus est:
![\[ B(x)=-x^2+128x-3952\]](/Generateur-Devoirs/2nde/Chap5/ex2/6.png)
- Montrer que pour tout nombre réel
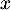 , on a
, on a
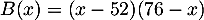 .
Déterminer alors le nombre de lots que doit produire et fabriquer la
société pour être rentable (pour avoir un bénéfice positif …).
.
Déterminer alors le nombre de lots que doit produire et fabriquer la
société pour être rentable (pour avoir un bénéfice positif …).
- Montrer que
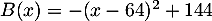 .
.
Etudier alors les variations de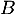 sur
sur ![$[0;64]$](/Generateur-Devoirs/2nde/Chap5/ex2/11.png) .
.
On admet pour la suite que la fonction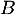 est décroissante sur
est décroissante sur 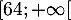 .
.
Dresser le tableau de variations de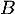 .
.
- Quel est le bénéfice maximal que peut espérer Monsieur Dupré ? Pour combien de lots fabriqués et vendus ?
Correction exercice
-
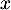 lots produits et vendus rapportent
lots produits et vendus rapportent 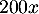 euros.
La production de ces
euros.
La production de ces 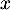 lots coûtent
lots coûtent 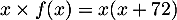 euros plus
3952 euros.
Ainsi, le bénéfice est
euros plus
3952 euros.
Ainsi, le bénéfice est
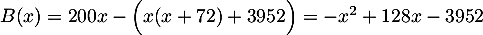 .
.
- En développant, on a
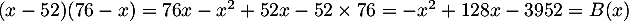 .
Ainsi, le bénéfice pour
.
Ainsi, le bénéfice pour  lots produits et vendus est
lots produits et vendus est
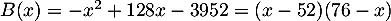 .
.
![\[
\begin{tabular}[t]{|c|ccccccc|}\hline
$x$&$-\infty$ & & $52$ & & $76$ & & $+\infty$ \\\hline
$x-52$ & & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & $|$ & $+$ &\\\hline
$76-x$ & & $+$ & $|$ & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$B(x)$& & $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
\end{tabular}
\]](/Generateur-Devoirs/2nde/Chap5/ex2_c/9.png)
La société est rentable lorsque le bénéfice est positif, soit donc lorsque le nombre de lots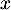 produits et vendus est
compris entre
produits et vendus est
compris entre 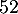 et
et 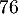 lots.
lots.
-
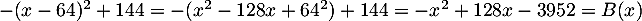 .
Ainsi, pour tout
.
Ainsi, pour tout 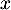 ,
, 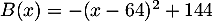 .
.
Soit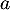 et
et 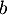 deux nombres quelconques de
deux nombres quelconques de ![$[0;64]$](/Generateur-Devoirs/2nde/Chap5/ex2_c/18.png) tels que
tels que
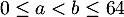 ,
,
alors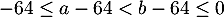 ,
,
donc,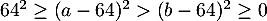 , en élevant au carré des nombres négatifs,
, en élevant au carré des nombres négatifs,
d'où,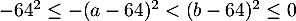 , en multipliant par
, en multipliant par 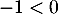
soit,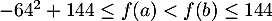
donc,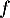 est croissante sur
est croissante sur ![$[0;64]$](/Generateur-Devoirs/2nde/Chap5/ex2_c/26.png)
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $0$ & & $64$ & & $+\infty$ \\\hline
& & & $144$ &&\\
$B(x)$ & & \Large{$\nearrow$}& &\Large{$\searrow$}& \\
& $-3952$ & &&&\\\hline
\end{tabular}
\]](/Generateur-Devoirs/2nde/Chap5/ex2_c/27.png)
- Le bénéfice maximum que peut espérer M. Duspré est de
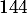 euros,
pour
euros,
pour 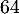 lots produits et vendus.
(remarque: pour
lots produits et vendus.
(remarque: pour 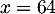 lots la
société est bien rentable, cf. question 1)).
lots la
société est bien rentable, cf. question 1)).
Cacher la correction
Voir aussi: