Exercice corrigé: Recette maximale pour une agence de voyage
Recette maximale
Seconde générale
Exercice corrigé de mathématiques: Exercice corrigé: Agence de voyage, son nombre de passagers et sa recette maximale
Exercice - énoncé:
Un voyagiste veut faire une promotion sur le vol Paris-Londre. Le
nombre de places disponibles est au maximum de 10200.
Partie A. Etude du nombre de passagers.
Cacher la correction
Le nombre ![]() de passagers intéressés est fonction du prix
de passagers intéressés est fonction du prix ![]() , en
euros, du billet :
, en
euros, du billet :
![]() .
.
Partie A. Etude du nombre de passagers.
- Calculer le nombre de passagers si le prix du billet est
fixé à 65euros.
- Calculer le prix du billet en supposant que 7200 passagers
sont intéressés.
- Que se passe-t-il si le billet est gratuit ? si le prix du
billet est de 85euros ?
- Quel est le sens de variation de la fonction
 sur l'intervalle
sur l'intervalle ![$ [0;85]$](/Generateur-Devoirs/1STG/Chap8/ex2_img5.png) ?
?
- Tracer la courbe représentative de la fonction
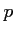 dans le
plan rapporté à un repère orthonogonal (unités graphiques: 1cm pour
5euros en abscisse et 1cm pour 500 passagers en ordonnées).
dans le
plan rapporté à un repère orthonogonal (unités graphiques: 1cm pour
5euros en abscisse et 1cm pour 500 passagers en ordonnées).
Retrouver graphiquement les résultats des questions 1. et 2.
Partie B. Etude de la recette.
- a. Montrer que la recette
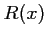 quand le billet vaut
quand le billet vaut 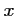 euros est donné par :
euros est donné par :
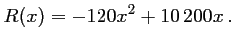
- b. Calculer la recette si le prix du billet est de 10euros, 42,50euros, 50euros et 60euros.
On donne, ci-contre, la courbe représentative de la fonction .
.
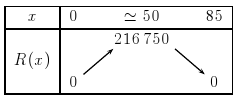
- a. Dresser le tableau de variation de la fonction
 .
.
- b. Déterminer graphiquement le prix du billet permettant d'avoir une recette maximale, et calculer le nombre de passagers correspondant.
![\begin{pspicture}(-100,40)(5,3)
\psaxes[linewidth=1.5pt,Dx=10,Dy=20]{->}(0,0)(0,...
...}
\put(5,0.5){Prix du}
\put(5,0.){billet}
\put(5,-0.5){(euros)}
\end{pspicture}](/Generateur-Devoirs/1STG/Chap8/ex2_img10.png)
- a. Montrer que la recette
Correction exercice
Partie A. Etude du nombre de passagers.
-
- 1. Si le prix du billet est fixé à 65euros,
il y a
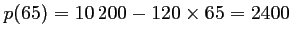 passagers.
passagers.
- 2. Si 7200 passagers sont intéressés, le prix
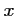 sera tel que
sera tel que
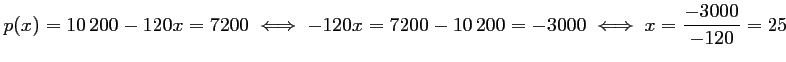 ,
soit un prix de 25 euros.
,
soit un prix de 25 euros.
- 3. Si le billet est gratuit, c'est-à-dire vaut
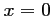 euros,
alors il y aura
euros,
alors il y aura
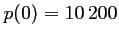 personnes intéressées,
c'est-à-dire le maximum de personnes.
personnes intéressées,
c'est-à-dire le maximum de personnes.
Si le billet est à 85 euros, il y aura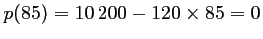 personne intéressée.
personne intéressée.
- 4. La fonction
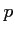 est une fonction affine dont le coefficient
directeur est
est une fonction affine dont le coefficient
directeur est 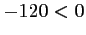 .
La fonction
.
La fonction 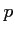 est donc décroissante sur l'intervalle
est donc décroissante sur l'intervalle ![$ [0;85]$](/Generateur-Devoirs/1STG/Chap8/ex2_c_img9.png) .
.
- 5.
![\begin{pspicture}(-100,2)(5,240)
\psaxes[linewidth=1.5pt,Dx=10,Dy=20]{->}(0,0)(0...
...(5,-0.5){(euros)}
\psline[linestyle=dashed](43,0)(43,216)(0,216)
\end{pspicture}](/Generateur-Devoirs/1STG/Chap8/ex2_c_img22.png)
On retrouve graphiquement que: - pour un prix de 65 euros, environ 2200 personnes sont intéressées;
- si 7200 passagers sont inéressés, le prix sera d'environ 25 euros.
Partie B. Etude de la recette.
-
- 1.
- a) Si le prix du billet est
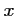 euros, alors il y aura
euros, alors il y aura
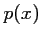 passagers, soit une recette de
passagers, soit une recette de
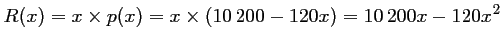
- b) Si le prix du billet est de:
- 10 euros, la recette est de
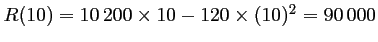 euros
euros
- 42,50 euros, la recette est de
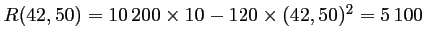 euros
euros
- 50 euros, la recette est de
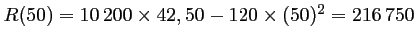 euros
euros
- 60 euros, la recette est de
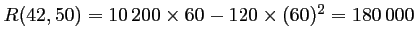 euros
euros
- 10 euros, la recette est de
2.
- a)
- b) Graphiquement le prix du billet permettant
d'avoir une recette maximale est d'environ 43 euros, pour une
recette d'environ 216000 euros, et
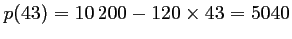 passagers.
passagers.
![\begin{pspicture}(-30,-1000)(100,11000)
\psline[arrowsize=6pt]{->}(0,0)(100,0)
...
...line[linestyle=dashed,arrowsize=5pt]{->}(0,7200)(25,7200)(25,0)
\end{pspicture}](/Generateur-Devoirs/1STG/Chap8/ex2_c_img10.png)
- a) Si le prix du billet est
Cacher la correction
Voir aussi: