Repérage dans le plan - Graphiques en Python


Pour pouvoir utiliser des fonctions graphiques en Python, il faut charger une bibliothèque.
Dans la suite, on utilisera Pylab qui est un module qui permet d'importer et d'utiliser aisément la bibliothèque grahique pyplot de matplotlib, ainsi que, à la fois, la bibliothèque numpy de calcul scentifique.
Chaque programme débutera par la ligne: 
from pylab import *

Utilisation et exemples

La fonction plot permet de tracer des points repérés par leurs coordonnées. Une fois les instructions et autres commandes graphiques indiquées, on finit par la commande show() qui affiche (montre) le résultat.
Par exemple 
from pylab import *
x=2;
y=3;
plot(x,y,'*r')
show()
Le troisième argument de la fonction plot désigne le symbole utilisé pour indiquer le point (ici une étoile *, ainsi qu'une couleur: r pour red, b pour blue, k pour black, g pour green, ... )
On peut placer plusieurs points en répétant l'étape précédente 
from pylab import *
x=2;y=3;plot(x,y,'*r')
x2=4;y2=5;plot(x2,y2,'+b')
x3=5;y3=8;plot(x3,y3,'og')
show()
Pour tracer plusieurs points, on peut préférer définir une liste de points, ce qui va permettre entre autre de relier les points entre eux, par exemple 
from pylab import *
x=[2,4,5]
y=[3,5,8]
plot(x,y)
show()

Exercices

Exercice 1:
  1. Écrire un programme qui affiche le triangle suivant:
  2. Écrire un programme qui affiche la figure suivante:

Exercice 2:
  1. Qu'affiche le programme suivant ? 
    for i in range(0,10):
    print(i)
    ( (re)voir éventuellement les boucles for, et plus précisément les boucles avec des entiers et range))

  2. Écrire un programme qui affiche la figure suivante
  3. Écrire un programme qui affiche la figure suivante
  4. Écrire un programme qui affiche la figure suivante
  5. Écrire un programme qui affiche la figure suivante
  6. Écrire un programme qui affiche la figure suivante

Exercice 3:
  1. Écrire un programme qui affiche les points A(-2;1), B(58;30) et C(122;61), et les trois segments [AB], [BC] et [AC] (respectivement en blue, noir et rouge).
    Ces trois points sont-ils alignés ?
  2. Observer de "plus près" le point B, en modifiant l'echelle grâce à xlim et ylim.
  3. Démontrer ce résultat par le calcul.

Exercice 4: Glissement le long d'une échelle: astroïde Ue poutre de 10m de haut est appuyée contre une échelle verticale.
Elle est initialement verticale, puis glisse sur le sol et tombe d'échelon en échelon jusqu'à se retrouver complètement à l'horizontal sur le sol.

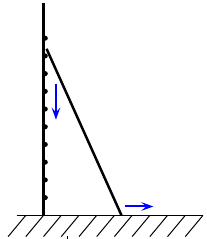
On se place dans un repère et on note A et B les points aux extrémités de la poutre:
  1. Donner les coordonnées de A et de B lorsque la poutre est verticale.
  2. Donner les coordonnées de A lorsque la poutre a glissé d'un échelon, et calculer les coordonnées de B correspondantes.
  3. Donner de même les coordonnées de A lorsque la poutre a glissé de deux échelons, et calculer les coordonnées de B correspondantes.
  4. La poutre a maintenant glissé de i échelons. Donner alors les coordonnées de B en fonction de i.
  5. Écrire un programme qui trace toutes les positions successives de la poutre (c'est-à-dire tous les segments [AB]), échelon après échelon, depuis sa position verticale jusqu'à sa position finale horizontale.
  6. Si B a comme coordonnées x et y, quelles sont les coordonnées du symétrique B' par rapport à l'axe des ordonnées.
    Compléter le programme précédent pour qu'il trace aussi les segments [AB'].
  7. Donner de même, pour A de coordonnées x et y, les coordonnées du symétrique A' par rapport à l'axe des ascisses.
    Compléter le programme précédent pour tracer qu'il trace aussi les segments [A'B] et [A'B'].

    La figure ainsi obtenu s'appelle une astroïde.

  8. On peut obtenir une figure plus détaillée en utilisant des échelons écartés de 50 cm seulement (au lieu de 1 m), ou encore de 10 cm …

Exercice 5: On reprend l'exercice précédent et la poutre qui glisse sur le sol, d'échelon en échelon.
Pour deux points de coordonnées A(xA ; yA) et B(xB ; yB) donner les coordonnées du point I qui est le milieu de [AB].

Tracer toutes les positions successives du milieu de lapoutre, lors de sa chute.

Exercice 6: On considère trois points A(1;2), B(6;1), et C(2;8).
  1. Tracer le triangle ABC.
  2. On rappelle qu'une médiane dans un triangle est une droite qui joint un sommet au milieu du côté opposé.
    Tracer les trois médianes du triangle ABC.
    Quel résultat retrouve-t-on ?


Quelques options utiles

Limites de la fenêtre graphique

On peut spécifier les bornes de la fenêtre graphique en utilisant les fonctions xlim et ylim, par exemple 
xlim(-5,10)
ylim(3,13)
permet de spécifier que l'axe des abscisses va de -5 à 10 et celui des ordonnées de 3 à 13.

On peut de plus dessiner un quadrillage avec la commande 
grid()
Que l'on précise ou non les valeurs minimales et maximales pour chaque axe, on peut préciser 
axis("equal")
qui permet d'avoir la même échelle en abscisse et en ordonnée, c'est-à-dire d'imposer au repère d'être orthonormé.

Style et couleur des traits - Symboles pour marquer les points

On peut spécifier le type des traits et leur couleur en option de la commande plot, par exemple 
plot(x,y,'--*r')
qui trace les points avec une étoile *, les relie avec des tirets, le tout en rouge (red).
Dans cette option on spécifie donc trois symboles:
  • le type de traits: - pour relier les points en trait plein, -- avec des tirets, -. avec des traits mixtes, : pour des pointillés
  • le type de symbole utilisé pour marquer chaque point: * pour une astérisque, o pour un rond, d pour un losange (diamond), + pour une croix
  • une couleur: r pour red, b pour blue, k pour black, g pour green, y pour yellow, m pour magenta
On peut utiliser toute combinaison de trois symboles, par exemple 
plot(x,y,'-dm')
plot(x,y,':og')

Épaisseur des traits

L'épaisseur des traits peut être spécifiée avec l'argument linewidth, par exemple 
plot(x,y,linewidth=5)

Titre et légende

Un titre à la fenêtre graphique se spécifie via la foction title, par exemple 
title("Un titre !")
La legende associée à chaque tracer se spécifie par un label dans la commande même de l'élément tracé, puis en indiquant d'ajoutant la légende, par exemple, 
plot(x1,y1,'-db',linewidth=2,label="Courbe 1")
plot(x2,y2,'--+k',linewidth=4,label="Courbe 2")
title("2 belles courbes")
legend()


Voir aussi:
Top

LongPage: h2: 3 - h3: 4