Equations de droites, intersection avec les axes et entre elles
Exercice corrigé - maths en seconde générale
Énoncé
On considère les droites  et
et 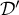 d'équations
d'équations
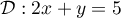 et
et
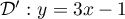 .
.
- Déterminer les coordonnées du point
 d'intersection
de
d'intersection
de  avec l'axe des ordonnées, et du point
avec l'axe des ordonnées, et du point
 d'intersection de
d'intersection de 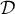 avec l'axe des abscisses.
avec l'axe des abscisses.
- Les droites
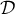 et
et 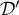 sont-elles parallèles ?
sont-elles parallèles ?
- Tracer dans un repère les droites
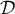 et
et 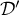 .
.
- Calculer les coordonnées des éventuels points d'intersection de
 et
et  .
.
Correction
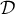 et
et 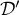 d'équations
d'équations
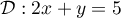 et
et
 .
.
Correction
On considère les droites- Soit
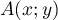 alors comme
alors comme 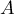 appartient à l'axe des ordonnées,
on a
appartient à l'axe des ordonnées,
on a  , et, comme
, et, comme 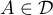 ,
, 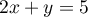 soit, avec
soit, avec  ,
,
 .
Ainsi on trouve
.
Ainsi on trouve  .
.
Soit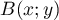 alors comme
alors comme 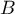 appartient à l'axe des abscisses,
on a
appartient à l'axe des abscisses,
on a  , puis comme
, puis comme 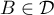 ,
, 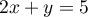 soit, avec
soit, avec 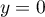 ,
,
 .
Ainsi, on trouve
.
Ainsi, on trouve  .
.
-
 et
et 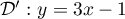 .
.
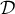 a pour coeeficient directeur
a pour coeeficient directeur  et
et 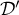 a pour coefficient directeur
a pour coefficient directeur  .
Ces coefficients directeurs sont différents, donc les droites
sont sécantes.
.
Ces coefficients directeurs sont différents, donc les droites
sont sécantes.
-
![\[\psset{unit=.7cm,arrowsize=7pt}
\begin{pspicture}(-1,-2)(4,5.5)
\psline{->}(-1.2,0)(4,0)
\psline{->}(0,-2)(0,6)
\multido{\i=-1+1}{7}{\psline(.1,\i)(-.1,\i)\rput(-.2,\i){\i}}
\multido{\i=-1+1}{5}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\psplot{-.5}{3}{-2 x mul 5 add}\rput(2.5,.8){$\mathcal{D}$}
\psplot{-.3}{2}{3 x mul 1 sub}\rput(2.3,4.6){$\mathcal{D}'$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap4/ex0_c/27.png)
- Soit
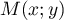 le point d'intersection de
le point d'intersection de 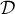 et
et  , alors on a
, alors on a
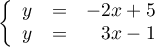
d'où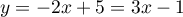 donc
donc
 ,
et alors
,
et alors 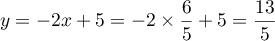 .
.
Ainsi, le point d'intersection est .
.
Tag:All
Voir aussi:
