Calcul approché d'intégrale
Méthodes des rectangles et des trapèzes
Méthode des rectangles
Exercice 1:
Calculer l'aire exacte de la surface ci-dessus et comparer avec l'approximation donnée.
Solution
L'aire est celle du domaine compris entre les droites (verticales) d'équations
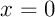 et
et 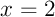 ,
et entre l'axe des abscisses et la courbe représentative de la fonction
,
et entre l'axe des abscisses et la courbe représentative de la fonction
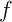 définie par l'expression
définie par l'expression
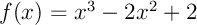 .
.
Une primitive de cette fonction est donnée par l'expression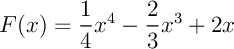 .
.
![\[\begin{array}{ll}\dsp\int_0^2 f(x)dx
&=\dsp\int_0^2 \left( x^3-2x^2+2 \right) dx \\&=\Bigl[\,F(x)\,\Bigr]_0^2 \\&=F(2)-F(0)\enar\]](IMG/CalculInt.png)
avec
![\[\begin{array}{ll}F(2)&=\dfrac14\tm2^4-\dfrac23\tm2^3+2\tm2\\&=4-\dfrac{2^4}3+4=\dfrac{8}3\enar\]](IMG/F2.png)
et
![\[F(0)=0\]](IMG/F0.png)
ce qui nous donne donc l'aire
![\[\int_0^2 f(x)dx=\dfrac83\simeq2,666\dots\]](IMG/Resultat.png)
Une primitive de cette fonction est donnée par l'expression
![\[\begin{array}{ll}\dsp\int_0^2 f(x)dx
&=\dsp\int_0^2 \left( x^3-2x^2+2 \right) dx \\&=\Bigl[\,F(x)\,\Bigr]_0^2 \\&=F(2)-F(0)\enar\]](IMG/CalculInt.png)
avec
![\[\begin{array}{ll}F(2)&=\dfrac14\tm2^4-\dfrac23\tm2^3+2\tm2\\&=4-\dfrac{2^4}3+4=\dfrac{8}3\enar\]](IMG/F2.png)
et
ce qui nous donne donc l'aire
![\[\int_0^2 f(x)dx=\dfrac83\simeq2,666\dots\]](IMG/Resultat.png)
Exercice 2:
Compléter le programme suivant pour qu'il calcule, et affiche, une valeur approchée de l'intégrale par la méthode des rectangles.
def f(x):
return x**3-2*x**2+2
a=0
b=2
n=int(input("Saisir n: "))
dx= ...
S=0
for k in range(n):
x= ...
S=S+ f( ... ) * dx
print("Valeur approchée:")
print(S) Exercice 3:
Exercice Bac S 2015: Pentes dans un skateparc, et surface à peindre.
Méthodes des trapèzes
Exercice 4:
Rappeler l'aire d'un trapèze et modifier le programme précédent pour calculer maintenant une valeur approchée de l'intégrale avec la méthode des trapèzes.
Comparer la vitesse de convergence des deux méthodes: quelle est l'erreur commise pour chaque méthode et n=10, n=100, n=1000, ... ?
Top