Calcul approché d'intégrale
Méthodes de Monté Carlo
Aire d'un disque: approximation de π à l'aide du hasard
Aire du rectangle 16
Nombre de points dedans: 0
Ratio: NaN
Ratio x Aire rectangle: NaN
Exercice 1:
- Le programme suivant permet de tirer un nombre x aléatoire, et uniformément, entre 0 et 1;
la variable y suivante est alors une variable aléatoire comprise entre -1 et 1.
En d'autres termes, y est une variable aléatoire qui suit la loi uniforme sur [-1;1].from random import random x=random() print(x) y=2*x-1 print(y) - Quelle est l'aire du cercle centré à l'origine et de rayon 1 ?
À quelle condition un point M(x;y) est-il à l'intérieur de ce cercle ? - Compléter le programme suivant
from random import random n=int(input("Nombre points ? n= ")) c=0 for i in range(n): x=2*random()-1 y=2*random()-1 if ( ... ): ... print("Nombre de points dans le disque:") print( ... ) print("Ratio:", ... ) print("Approximation de l'aire du disque:") print( ... )
Aire sous une courbe: intégrale
Nombre de points dedans:
Ratio:
Aire:
Exercice 2:
- Décrire algébriquement le domaine sur la figure précédente compris entre les abscisses 0 et 2, et entre l'axe des abscisses et la courbe représentative de la fonction
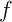 .
SolutionIl s'agit du domaine compris entre les droites (verticales) d'équations
.
SolutionIl s'agit du domaine compris entre les droites (verticales) d'équations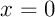 et
et 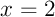 ,
et entre l'axe des abscisses et la courbe représentative de la fonction
,
et entre l'axe des abscisses et la courbe représentative de la fonction
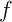 définie par l'expression
c'est-à-dire le domaine défini par
définie par l'expression
c'est-à-dire le domaine défini par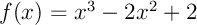 .
.![\[
\mathcal{D}=\left\{ \begin{array}{l} \ \\ M(x;y) \text{ tel que }
\left\{\bgar{ll}
&0\leqslant x\leqslant 2\\ \text{et}&0\leqslant y\leqslant f(x)\end{array}
\right.\\ \ \enar\ra\]](IMG/Domaine.png)
- Calculer l'aire exacte de ce domaine.
SolutionUne primitive de la fonction
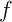 définie par l'expression
est donnée par l'expression
définie par l'expression
est donnée par l'expression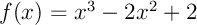 .et l'aire du domaine est alors l'intégrale
.et l'aire du domaine est alors l'intégrale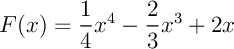 .
.![\[\begin{array}{ll}\dsp\int_0^2 f(x)dx
&=\dsp\int_0^2 \left( x^3-2x^2+2 \right) dx \\&=\Bigl[\,F(x)\,\Bigr]_0^2 \\&=F(2)-F(0)\enar\]](IMG/CalculInt.png)
avec
![\[\begin{array}{ll}F(2)&=\dfrac14\tm2^4-\dfrac23\tm2^3+2\tm2\\&=4-\dfrac{2^4}3+4=\dfrac{8}3\enar\]](IMG/F2.png)
et
![\[F(0)=0\]](IMG/F0.png)
ce qui nous donne donc l'aire
![\[\int_0^2 f(x)dx=\dfrac83\simeq2,666\dots\]](IMG/Resultat.png)
- Compléter le programme suivant pour qu'il affiche une approximation de l'intégrale précédente:
from random import random def f(x): return x**3-2*x**2+2 n=int(input("Nombre points ? n= ")) c=0 for i in range(n): x= ... * random() ... y= ... * random() ... if ( ... ): ... print("Nombre de points sous la courbe:") print( ... ) print("Ratio:", ... ) print("Approximation de l'intégrale:") print( ... )
Exercice 3:
Exercice Bac S (septembre 2019): Intégrale gaussienne, encadrements et algorithme de Monté Carlo.
Top