Exercices corrigés - Algorithme
Minimisation discrète d'un coût
Exercice corrigé de mathématiques: Exercices corrigés - Algorithme d'optimisation (minimisaton) du coût de fabrication d'un objet
Exercice - énoncé:
Dans une usine, le coüt de fabrication, en milliers d'euros,
de 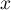 objets,
pour un nombre d'objets compris entre 1 et 5, est donné
par l'expression:
objets,
pour un nombre d'objets compris entre 1 et 5, est donné
par l'expression:
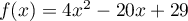
Dans une usine, le coüt de fabrication, en milliers d'euros, de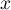 objets,
pour un nombre d'objets compris entre 1 et 5, est donné
par l'expression:
objets,
pour un nombre d'objets compris entre 1 et 5, est donné
par l'expression:
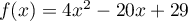
1.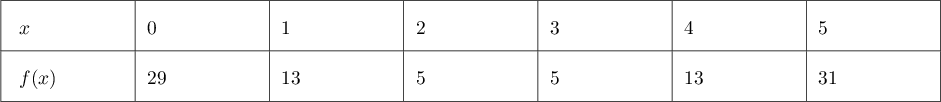
Finalement, on affiche
2, 5
.
Cet algorithme permet de calculer et d'afficher la plus petite
valeur prise par  lorsque
lorsque 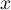 est un entier compris entre
est un entier compris entre 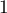 et
et 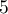 , et la valeur de
, et la valeur de 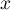 correspondante:
c'est le coüt de fabrication minimal.
correspondante:
c'est le coüt de fabrication minimal.
Cacher la correction
- 1. Compléter le tableau de valeurs de la fonction
 suivant:
suivant:
|
Pour Si Afficher Fin Fin Afficher |
Correction exercice
Dans une usine, le coüt de fabrication, en milliers d'euros, de
1.
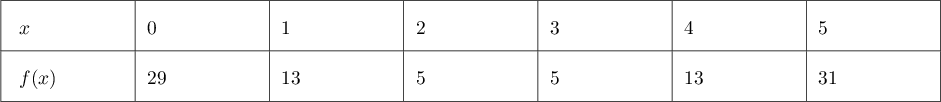
|
2.
Pour I=1: Pour I=2: Pour I=3: Pour I=4: Pour I=5: |
Cacher la correction
Voir aussi: