Simulation de la propagation monodimensionnelle d'une onde
Discrétisation en espace et en temps
On s'intéresse par la suite à la résolution numérique de ce problème lorsque le domaine D est un segment [0 , L].Ce cas 1-D (une dimension) correspond par exemple à la simulation du mouvement d'une corde (de piano ou de guitare par exemple), ou de l'amplitude d'un champ électrique ou magnétique en polarisation TE ou TM.
Le domaine géométrique dans lequel l'onde peut se propager est le segment [0 , L].
On s'interesse donc à l'amplitude de l'onde f (x, t) pour x∈[0 , L] et t∈[0 , T].
Pour approximer les valeurs de l'amplitude de l'onde, nous allons utiliser la méthode numérique dite des différences finies.
On se donne tout d'abord pour cela une "grille" régulière de calcul, c'est-à-dire une discrétisation de l'ensemble [0 , L] × [0 , T].
On découpe pour cela notre longueur L en Nx segments de longueurs δx et on construit la suite
xk = kδx pour k = 0, …, Nx
et de même pour l'intervalle de temps [0 , T] qu'on découpe en Nt segments de longueurs δt en construisant la suite
tk = kδt pour k = 0, …, Nt
Cette grille étant donnée, on cherche à calculer les valeurs de l'amplitude f "seulement" aux noeuds de la grille. On notera pour cela
fi,j = f (xi, tj)
Approximations des dérivées partielles secondes
La deuxième étape est l'approximation des dérivées partielles de f à l'aide des éléments fi,j. Cela peut s'effectuer à l'aide de la formule de Taylor, par exemple pour la dérivée selon x:
f (x+δx, t)
= f (x,t)
+ δx∂f∂x(x, t)
+
δx22∂2f∂x2(x, t)
+ O(δx3)
ou, en d'autres termes, en se plaçant en xi et tj
fi+1, j
= fi,j
+ δx
∂fi,j∂x
+
δx22∂2fi,j∂x2
+ O(δx3)
Cette dernière formule relie, pour δx 0, les valeurs de l'amplitude f et de sa dérivée et dérivée seconde.
On peut approximer de la même façon en considérant cette fois un saut en arrière de δx:
f (x−δx, t)
= f (x,t)
− δx∂f∂x(x, t)
+
δx22∂2f∂x2(x, t)
+ O(δx3)
soit encore, en se plaçant à nouveau en xi et tj
fi−1, j
=
fi,j
− δx
∂fi,j∂x
+
δx22∂2fi,j∂x2
+ O(δx3)
En ajoutant ces deux dernières relations exprimant fi+1, j et fi−1, j, on fait disparître les dérivées premières et on obtient
fi+1, j + fi−1, j
=
2fi,j
+
δx2∂2fi,j∂x2
+ O(δx3)
d'où
∂2fi,j∂x2
=
fi+1, j + fi−1, j − 2fi,j
δx2
+ O(δx)
En peut procéder de la même façon pour les dérivées par rapport au temps t, et on obtient de manière analogue,
∂2fi,j∂t2
=
fi, j+1 + fi, j−1 − 2fi,j
δt2
+ O(δt)
Équation de Helmholtz discrétisée
En utilise alors ces deux dernières relations dans l'équation de Helmoltz, ou équation des ondes, en 1-D:
∂2f
∂t2
(x,t)
− c2
∂2f
∂x2
(x,t)
= 0
soit, en xi et tj
∂2fi, j
∂t2
− c2
∂2fi, j
∂x2
= 0
et en utilisant alors les deux relations obtenues à partir des formules de Taylor, on obtient maintenant la relation de récurrence:
fi ,j+1
=
− fi ,j−1
+ γ fi+1 ,j
+ γ fi−1 ,j
−2 (1−γ) fi,j
en notant
γ =
c
δt
δx
2
Il ne reste plus alors qu'à initialiser la suite fi, j, ce qui se fait en reprenant la modélisation complète de la propagation de l'onde avec, en particulier, les conditions aux limites
Conditions initiales
Pour commencer, on peut prendre g = 0. Cette condition modélise une paroi infiniment dure; l'onde y sera totalement réfléchie.La fonction h1 modélise l'état initial de l'onde, à l'instant t = 0.
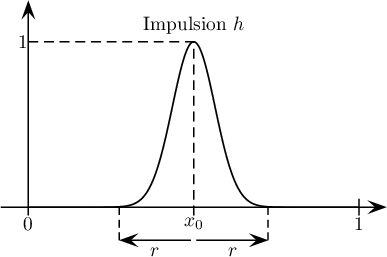
On utilisera par la suite dans les simulations la fonction h, infiniment régulière (c'est-à-dire de classe C∞)
h1(x) =
Aexp
−
1
|(x−x0)2−r2|
si |x−x0|≤r
0
sinon
où A est une constante et permet de normaliser l'amplitude initiale, et x0 le centre de la "cloche" et r > 0 sa largeur>.
La fonction h2 modélise l'"impulsion", ou la vitesse, initiale donnée à l'onde. On choisira dans les simulations suivantes h2 = 0