Devoir corrigé de maths en Terminale générale, spécialité mathématiques
Intégrales
Devoir de mathématiques, et corrigé, posé en spé maths, terminale générale, année scolaire 2022/2023Exercice 1: Quelques calculs d'intégrales
Calculer les intégrales:
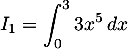 ;
;
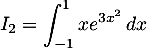 ;
;
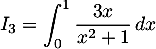 ;
;
À l'aide d'une intégration par parties, calculer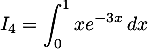
À l'aide d'une intégration par parties, calculer
Exercice 2: Exponentielle et intégrales (Bac 2014)
Sur le graphique ci-dessous, on a tracé, dans un repère orthonormé
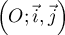 , une courbe
, une courbe 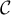 et la droite
et la droite 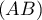 où
où 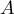 et
et 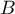 sont les points de coordonnées respectives
sont les points de coordonnées respectives 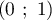 et
et
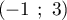 .
.
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-3,-2.2)(3,3.5)
\psline[linewidth=1pt]{->}(-3,0)(3,0)
\psline[linewidth=1pt]{->}(0,-2.2)(0,3.8)
\rput(0,1){$\tm$}\rput(-1,3){$\tm$}
\uput[ur](0,1){$A$}\uput[l](-1,3){$B$}
\uput[dl](0,0){O}
\psline[linewidth=1.6pt]{->}(0,0)(1,0)\uput[d](0.5,0){$\vec{i}$}
\uput[d](-1,0){$- 1$}\uput[r](0,3){3}
\psline[linewidth=1.6pt]{->}(0,0)(0,1)\uput[l](0,0.5){$\vec{j}$}
\uput[d](-2,-1.2){$\mathcal{C}$}
\psline[linestyle=dashed](-1,0)(-1,3)(0,3)
\psplot[plotpoints=5000,linewidth=1.25pt,linecolor=blue]{-2.5}{2.5}{1 x add x 3 mul 2.71828 x dup mul exp div sub}
\psplot{-1.4}{1.5}{1 x 2 mul sub}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/8.png)
On désigne par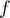 la fonction dérivable sur
la fonction dérivable sur 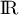 dont la courbe
représentative est
dont la courbe
représentative est 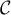 .
.
On suppose, de plus, qu'il existe un réel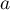 tel que pour tout réel
tel que pour tout réel 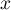 ,
,
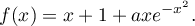
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-3,-2.2)(3,3.5)
\psline[linewidth=1pt]{->}(-3,0)(3,0)
\psline[linewidth=1pt]{->}(0,-2.2)(0,3.8)
\rput(0,1){$\tm$}\rput(-1,3){$\tm$}
\uput[ur](0,1){$A$}\uput[l](-1,3){$B$}
\uput[dl](0,0){O}
\psline[linewidth=1.6pt]{->}(0,0)(1,0)\uput[d](0.5,0){$\vec{i}$}
\uput[d](-1,0){$- 1$}\uput[r](0,3){3}
\psline[linewidth=1.6pt]{->}(0,0)(0,1)\uput[l](0,0.5){$\vec{j}$}
\uput[d](-2,-1.2){$\mathcal{C}$}
\psline[linestyle=dashed](-1,0)(-1,3)(0,3)
\psplot[plotpoints=5000,linewidth=1.25pt,linecolor=blue]{-2.5}{2.5}{1 x add x 3 mul 2.71828 x dup mul exp div sub}
\psplot{-1.4}{1.5}{1 x 2 mul sub}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/8.png)
On désigne par
On suppose, de plus, qu'il existe un réel
-
- Justifier que la courbe
 passe par le point
passe par le point  .
.
- Déterminer le coefficient directeur de la droite
 .
.
- Démontrer que pour tout réel
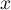 ,
,
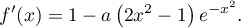
- On suppose que la droite
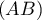 est tangente à la courbe
est tangente à la courbe
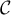 au point
au point 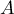 .
.
Déterminer la valeur du réel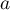 .
.
- Justifier que la courbe
- D'après la question précédente, pour tout réel
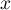 ,
,
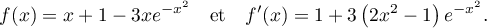
- Démontrer que pour tout réel
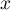 de l'intervalle
de l'intervalle
![$]- 1~;~0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/27.png) ,
,  .
.
- Démontrer que pour tout réel
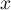 inférieur ou égal à
inférieur ou égal à 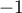 ,
,
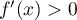 .
.
- Démontrer qu'il existe un unique réel
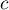 de l'intervalle
de l'intervalle
![$\left[- \dfrac{3}{2}~;~- 1\right]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole/33.png) tel que
tel que 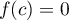 .
Justifier que
.
Justifier que 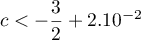 .
.
- Démontrer que pour tout réel
- On désigne par
 l'aire, exprimée en unités d'aire,
du domaine défini par:
l'aire, exprimée en unités d'aire,
du domaine défini par:
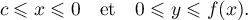
- Écrire
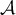 sous la forme d'une intégrale.
sous la forme d'une intégrale.
- On admet que l'intégrale
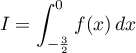 est une valeur approchée de
est une valeur approchée de 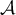 à
à 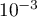 près.
près.
Calculer la valeur exacte de l'intégrale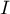 .
.
- Écrire
Correction exercice 2
Bac S - métropole, 11 septembre 2014 - 5 points
Cacher la correction
Bac S - métropole, 11 septembre 2014 - 5 points
-
- On a
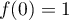 ce qui montre que le point de coordonnées
ce qui montre que le point de coordonnées
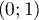 , c'est-à-dire
, c'est-à-dire 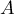 , appartient à
, appartient à 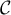 .
.
- Le coefficient directeur de la droite
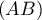 est
est
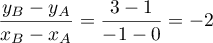 .
.
-
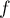 est de la forme
est de la forme
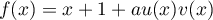 ,
avec
,
avec 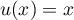 donc
donc 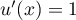 et
et 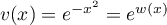 donc
donc 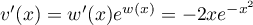 .
.
Ainsi,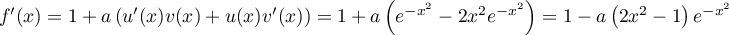 .
.
- Si la droite
 est tangente à la courbe
est tangente à la courbe  au
point
au
point 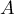 d'abscisse
d'abscisse 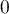 , alors le coefficient directeur de
, alors le coefficient directeur de 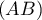 est
est 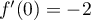 .
Ainsi,
.
Ainsi, 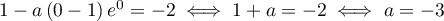
- On a
- On a donc, avec
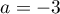 ,
,
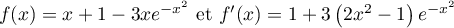 .
.
- Pour tout réel
![$x\in]-1;0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/23.png) ,
, 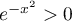 et
et
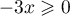 , donc
, donc 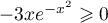 .
.
Pour tout![$x\in]-1;0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/27.png) ,
, 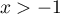 , donc
, donc 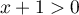 ,
alors, par addition,
,
alors, par addition, 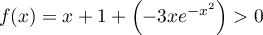 .
.
- Pour
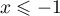 ,
, 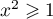 ,
donc,
,
donc, 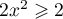 et
et 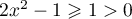 .
Ainsi,
.
Ainsi, 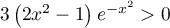 et alors
et alors
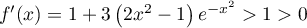 .
.
- Sur
![$] -\infty\,;\,-1]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/37.png) ,
, 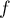 est dérivable donc continue,
avec
est dérivable donc continue,
avec 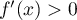 donc la fonction
donc la fonction 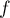 est
strictement croissante sur cet intervalle donc aussi sur l'intervalle
est
strictement croissante sur cet intervalle donc aussi sur l'intervalle
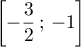 .
.
Or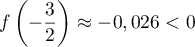 et
et 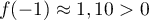 donc, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
l'équation
donc, d'après le corollaire du théorème des valeurs
intermédiaires (ou théorème de la bijection),
l'équation 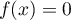 admet une solution unique
admet une solution unique 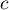 dans l'intervalle
dans l'intervalle
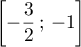 .
.
Or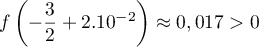 donc
donc 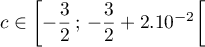 et donc
et donc 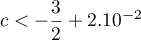 .
.
- Pour tout réel
-
- Comme
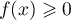 sur
sur ![$[c;0]](/Generateur-Devoirs/TS/ChapIntegration/ex2014-Septembre-Metropole_c/51.png) ,
alors
,
alors 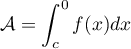 .
.
- La fonction
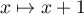 a pour primitive la fonction
a pour primitive la fonction
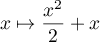 .
.
La fonction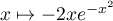 (forme
(forme 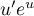 ) a pour
primitive la fonction
) a pour
primitive la fonction 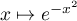 donc la fonction
donc la fonction 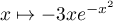 a pour primitive la fonction
a pour primitive la fonction
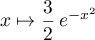 .
.
La fonction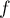 a donc pour primitive la fonction
a donc pour primitive la fonction 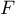 définie par
définie par 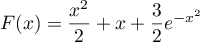 .
.
On a alors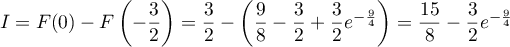
- Comme
Cacher la correction
Exercice 3: Logarithme et son carré, aire (IPP) et distance maximale (Bac 2008)
Les courbes C et C' données ci-dessous représentent respectivement, dans un repère orthonormal 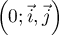 , les fonctions
, les fonctions 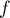 et
et 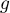 définies sur l'intervalle
définies sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/4.png) par
par 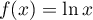 et
et 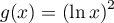 .
.
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
- On cherche à déterminer l'aire A (en unités d'aire) de la partie grisée.
On note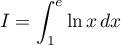 et
et 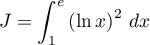 .
.
- Vérifier que la fonction
 définie sur l'intervalle
définie sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/11.png) par
par
 est une primitive de la fonction logarithme népérien.
En déduire
est une primitive de la fonction logarithme népérien.
En déduire 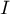 .
.
- Démontrer à l'aide d'une intégration par partie que
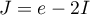 .
.
- Donner la valeur de A.
- Vérifier que la fonction
- Pour
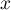 appartenant à l'intervalle
appartenant à l'intervalle ![$[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/16.png) , on note
, on note 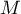 le point de la courbe C d'abscisse
le point de la courbe C d'abscisse 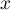 et
et  le point de la courbe C' de même abscisse.
le point de la courbe C' de même abscisse.
Pour quelle valeur de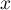 la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
Correction exercice 3
Bac juin 2008
Cacher la correction
Bac juin 2008
-
- On dérive:
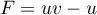 avec
avec 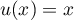 donc
donc  et
et 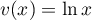 donc
donc  ,
,
et alors,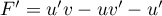 ,
,
soit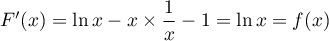
ce qui montre que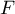 est bien une primtive de
est bien une primtive de 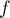 .
.
On en déduit
![\[\begin{array}{ll}I&=\dsp\int_1^e\ln x\,dx
=\Bigl[\,F(x)\,\Bigr]_1^e
=F(e)-F(1)\\[1em]
&=\left( e\ln e-e\rp-\left( 1\ln 1-1\rp
=1\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/10.png)
- On pose
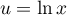 donc
donc 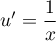 et
et 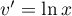 donc
donc 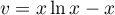 et et alors, en intégrant par parties,
et et alors, en intégrant par parties,
![\[\begin{array}{ll}J&=\Bigl[\ln x\left( x\ln x-x\rp\Bigr]_1^e
-\dsp\int_1^e\dfrac1x\left( x\ln x-x\rp\\[1em]
&=0-\dsp\int_1^e\lp\ln x-1\rp\,dx\\[1em]
&=-\dsp\int_1^e\ln x\,dx+\int_1^e1dx\\[1em]
&=-I+e-1=e-2I\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/15.png)
car .
.
- On en déduit la valeur de A:
![\[\begin{array}{ll}A&=\dsp\int_1^e\left( f(x)-g(x)\rp\,dx\\[1em]
&=\dsp\int_1^ef(x)\,dx-\int_1^eg(x)\,dx\\[1em]
&=I-J
=1-\left( e-2I\rp\\
&=1-\left( e-2\rp=3-e\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/17.png)
- On dérive:
- Pour
![$x\in[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/18.png) , on a
, on a
![\[\begin{array}{ll}MN&=d(x)=f(x)-g(x)\\[.5em]&=\ln x-\lp\ln x\rp^2\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/19.png)
Pour trouver le maximum de cette fonction, il suffit de connaître ses variations.
On a
![\[d'(x)=\dfrac1x-2\dfrac1x\ln x=\dfrac1x\lp1-2\ln x\rp\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/20.png)
avec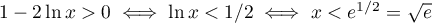 et donc
et donc
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$1$ && $\sqrt{e}$ && $e$\\\hline
$1/x$ && $+$ &$|$&$+$&\\\hline
$1-2\ln x$ && $+$ &\zb&$-$&\\\hline
$d'(x)$ && $+$ &\zb&$-$&\\\hline
&&&$d\lp\sqrt{e}\rp$&&\\
$d$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/22.png)
La distance est donc maximale en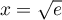 et cette distance maximale est
et cette distance maximale est
![\[d\lp\sqrt{e}\rp=\ln\sqrt{e}-\lp\ln\sqrt{e}\rp^2
=\dfrac12-\lp\dfrac12\rp^2=\dfrac14\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/24.png)
Cacher la correction
Voir aussi:
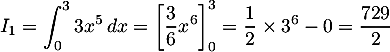
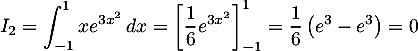
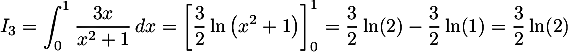
![\[\begin{array}{ll}I_4&=\dsp\int_0^1xe^{-3x}\,dx\\[1em]
&=\left[ -\dfrac13xe^{-3x}\rb_0^1-\dsp\int_0^1-\dfrac13e^{-3x}\,dx\\[1em]
&=-\dfrac13e^{-3}-\lb\dfrac19e^{-3x}\rb_0^1\\[1em]
&=-\dfrac13e^{-3}-\lp\dfrac19e^{-3}-\dfrac19e^0\rp\\[1em]
&=-\dfrac49e^{-3}+\dfrac19
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex0b_c/8.png)