Trigonométrie: fonction tangente
Exercice corrigé - Spécialité maths, terminale générale
Soit 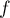 la fonction tangente, définie sur
la fonction tangente, définie sur
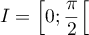 par
par
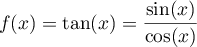 .
.
- Montrer que, pour tout
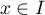 ,
,
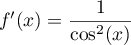 et que
et que
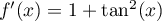 .
.
- Exprimer, pour tout
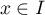 ,
, 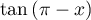 puis
puis 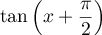 en fonction de
en fonction de 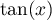 .
.
Correction
Soit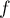 la fonction tangente, définie sur
la fonction tangente, définie sur
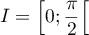 par
par
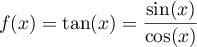 .
.
Cacher la correction
Soit
- On a
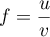 , avec
, avec
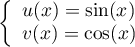 ,
donc
,
donc
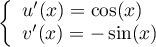 ,
et alors,
,
et alors, 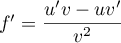 ,
,
soit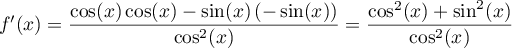 .
.
Comme, pour tout réel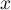 ,
, 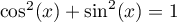 ,
on a alors
,
on a alors 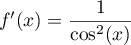 .
.
On peut aussi écrire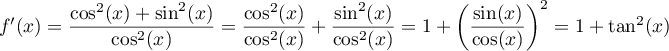 .
.
- Pour tout réel
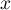 , on a
, on a 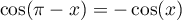 et
et 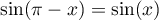 .
.
Ainsi, pour tout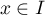 ,
,
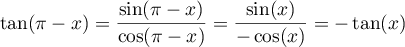 .
.
De même, pour tout réel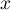 , on a
, on a 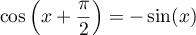 et
et 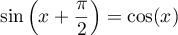 .
.
Ainsi, pour tout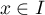 ,
,
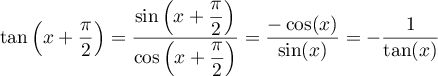 .
.
Cacher la correction
Tag:Trigonométrie
Voir aussi:
