Exercice corrigé Bac, Asie 2013: un exercice complet sur les suites, avec un algorithme
Suites récurrentes - Algorithme et limite
Exercice corrigé de mathématiques: Exercice corrigé Bac, Asie 2013: un exercice complet sur les suites récurrentes, démonstration par récurrence, et algorithme
Exercice - énoncé:
Partie A
On considère la suite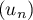 définie par:
définie par: 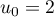 et, pour tout entier naturel
et, pour tout entier naturel 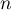 :
:
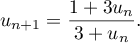
On admet que tous les termes de cette suite sont définis et strictement positifs.
Partie B
On considère la suite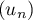 définie par:
définie par: 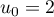 et, pour tout entier naturel
et, pour tout entier naturel 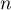 :
:
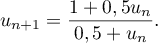
On admet que tous les termes de cette suite sont définis et strictement positifs.
Partie A
Partie B
Cacher la correction
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- Démontrer par récurrence que, pour tout entier naturel
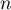 , on a :
, on a : 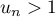 .
.
-
- Établir que, pour tout entier naturel
 , on a:
, on a: 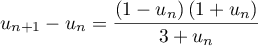 .
.
- Déterminer le sens de variation de la suite
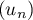 .
.
En déduire que la suite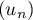 converge.
converge.
- Établir que, pour tout entier naturel
Partie B
On considère la suite
On admet que tous les termes de cette suite sont définis et strictement positifs.
- On considère l'algorithme suivant :

Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour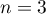 . Les valeurs de
. Les valeurs de 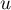 seront arrondies au millième.
seront arrondies au millième.
![\begin{tabular}{|*4{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.4cm]{0.3cm}{-0.8cm}
$u$&&&\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/18.png)
- Pour
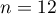 , on a prolongé le tableau précédent et on a obtenu :
, on a prolongé le tableau précédent et on a obtenu :
![\begin{tabular}{|c|*{9}{p{1.3cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&4&5&6&7&8&9&10&11&12\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&\footnotesize{1,0083}&\footnotesize{0,9973}&\footnotesize{1,0009}&\footnotesize{0,9997}&\footnotesize{1,0001}&\footnotesize{0,99997}&\footnotesize{1,00001}&\footnotesize{0,999996}&\footnotesize{1,000001}\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie/20.png)
Conjecturer le comportement de la suite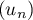 à l'infini.
à l'infini.
- On considère la suite
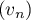 définie, pour tout entier naturel
définie, pour tout entier naturel 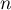 , par :
, par :  .
.
- Démontrer que la suite
 est géométrique de raison
est géométrique de raison  .
.
- Calculer
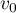 puis écrire
puis écrire 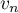 en fonction de
en fonction de 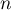 .
.
- Démontrer que la suite
-
- Montrer que, pour tout entier naturel
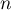 , on a:
, on a: 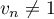 .
.
- montrer que, pour tout entier naturel
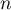 , on a:
, on a: 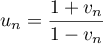 .
.
- Déterminer la limite de la suite
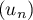 .
.
- Montrer que, pour tout entier naturel
Correction exercice
Partie A
- Initialisation : la relation est vraie au rang
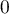 ;
;
Hérédité : supposons qu'il existe un naturel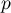 tel que
tel que 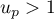 .
.
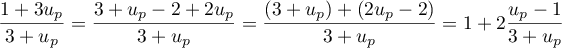 .
.
Par hypothèse de récurrence on a:
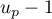 et comme
et comme 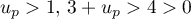 donc son inverse
donc son inverse 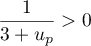 et finalement
et finalement 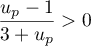 , c'est-à-dire que
, c'est-à-dire que 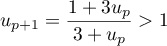
Conclusion: on a démontré, d'après le principe de récurrence, que pour tout entier naturel ,
, 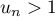 .
.
-
- Pour tout entier naturel
 ,
, 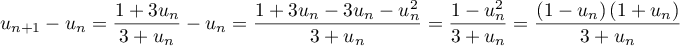 .
.
- On sait que pour tout entier
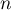 ,
, 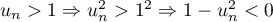 et comme
et comme 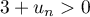 , on a
finalement
, on a
finalement 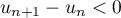 , ce qui signifie que la suite
, ce qui signifie que la suite 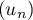 est décroissante.
est décroissante.
La suite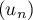 est décroissante et minorée par
est décroissante et minorée par 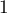 : elle converge donc vers une limite supérieure ou égale à
: elle converge donc vers une limite supérieure ou égale à 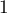 .
.
- Pour tout entier naturel
Partie B
-
![\begin{tabular}{|*{4}{p{1.5cm}|}}\hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$i$&1&2& 3\\ \hline
\rule[1.3cm]{0.3cm}{-0.8cm}
$u$&0,800&1,077&0,976\\ \hline
\end{tabular}](/Generateur-Devoirs/TS/ChapSuites/ex113.Asie_c/22.png)
- La suite semble converger vers
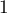 .
.
-
-
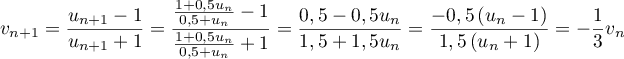 .
.
La suite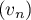 est donc géométrique de raison
est donc géométrique de raison 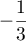 .
.
- On a
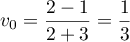 .
.
On sait qu'alors pour tout naturel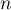 ,
, 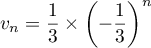 .
.
-
-
- Quel que soit le naturel
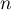 ,
, 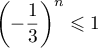 ,
donc
,
donc 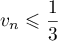 et par conséquent
et par conséquent 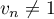 .
.
-
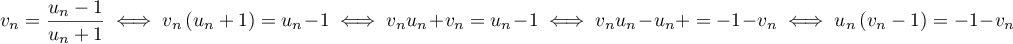 et comme
et comme 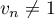 ,
,
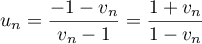 .
.
- Comme
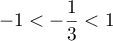 , on sait que
, on sait que 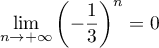 , soit
, soit 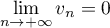 , donc d'après le résultat précédent
, donc d'après le résultat précédent 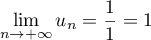 .
.
- Quel que soit le naturel
Cacher la correction
Voir aussi: