Exercice corrigé - Produit scalaire - Equations de cercles
Equations de cercles
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Produit scalaire - Equations de cercles
Exercice - énoncé:
Le plan est rapporté à un repère
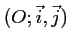 .
.
On écrit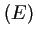 sous forme canonique:
sous forme canonique:
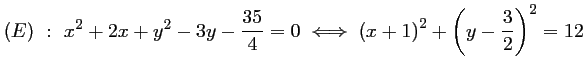 .
.
On considère l'équation
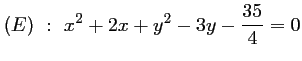 .
.
Montrer que ![]() est une équation de cercle, dont on déterminera le
centre et le rayon.
est une équation de cercle, dont on déterminera le
centre et le rayon.
Correction exercice
On écrit
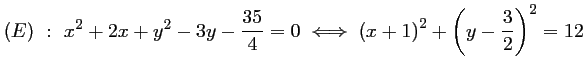 .
.
Il s'agit donc d'une équation du cercle de centre
 et de rayon
et de rayon
![]() .
.
Voir aussi: