Exercice corrigé - Second degré: Intersection d'une parabole et d'une droite
Intersection d'une parabole et d'une droite
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé sur Second degré - Recherche de l'intersection de deux courbes: une parabole et d'une droite
Exercice - énoncé:
Soit la fonction 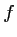 définie sur
définie sur
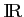 par
par
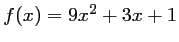 .
On note
.
On note
 la parabole représentant graphiquement
la parabole représentant graphiquement 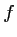 dans
un repère.
dans
un repère.
Cacher la correction
- 1)
Pour
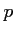 un nombre réel, on note
un nombre réel, on note
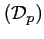 la droite
d'équation
la droite
d'équation 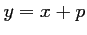 .
.
Pour quelles valeurs de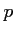 la droite
la droite
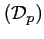 coupe-t-elle
la parabole en un seul point ? en deux points disctincts ?
coupe-t-elle
la parabole en un seul point ? en deux points disctincts ?
- 2)
Pour
 un nombre réel, on note
un nombre réel, on note
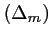 la droite
d'équation
la droite
d'équation 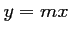 .
.
Pour quelles valeurs de la droite
la droite
 coupe-t-elle la
parabole en un unique point ?
coupe-t-elle la
parabole en un unique point ?
Correction exercice
- 1)
La parabole coupe la droite
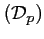 aux éventuels
points d'abscisse
aux éventuels
points d'abscisse 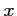 tel que
tel que  ,
soit
,
soit
 , ou encore
, ou encore
 .
.
Le discriminant de cette équation du second degré est :
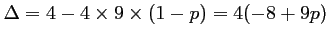 .
.
La parabole coupe cette droite en un seul point si et seulement si
 , soit
, soit 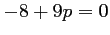 , et donc si et seulement si
, et donc si et seulement si
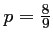 .
.
La parabole coupe cette droite en deux points distincts si et seulement si
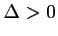 , c'est-à-dire si et seulement si
, c'est-à-dire si et seulement si
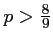 .
.
- 2)
La parabole coupe la droite
 aux éventuels
points d'abscisse
aux éventuels
points d'abscisse 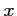 tel que
tel que 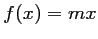 ,
soit
,
soit
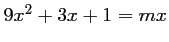 , ou encore
, ou encore
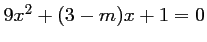 .
.
La parabole coupe cette droite en un unique point si et seulement si le discriminant de cette équation est nul:
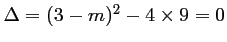 , soit
, soit
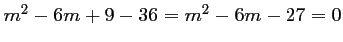 .
.
Le discriminant de cette dernière équation est
 . Elle admet donc deux solutions réelles
distinctes
. Elle admet donc deux solutions réelles
distinctes
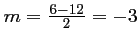 et
et
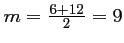 .
.
Finalement, la parabole coupe
 en un seul point pour
en un seul point pour
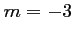 et
et 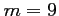 .
.
Cacher la correction
Voir aussi: