Exercice corrigé: Position relative de deux courbes
Position relative de deux courbes
Seconde générale
Exercice corrigé de mathématiques: Exercice corrigé: Calcul algébrique et étude de la position relative de deux courbes
Exercice - énoncé:
On considère les fonctions
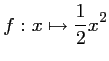 et
et
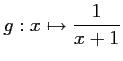 .
.
Le but de l'exercice est de comparer les positions des courbes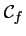 et
et
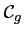 représentatives des fonctions
représentatives des fonctions 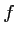 et
et 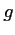 .
.
Cacher la correction
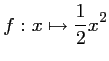 et
et
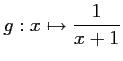 .
.
Le but de l'exercice est de comparer les positions des courbes
- 1)
Déterminer l'ensemble de définition des fonctions
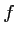 et
et
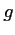 .
.
- 2)
Montrer que, pour tout nombre
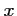 réel,
réel,
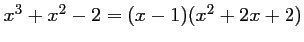 .
.
- 3)
Montrer que pour tout nombre
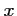 réel,
réel,
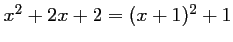 .
.
En déduire le signe de l'expression
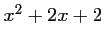 .
.
- 4)
A l'aide de ce qui précède, déterminer la position relative
des courbes
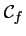 et
et
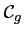 .
.
Correction exercice
- 1)
Dans l'expression de
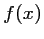 ,
, 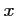 peut prendre n'importe
quelle valeur réelle:
peut prendre n'importe
quelle valeur réelle:
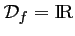 , tandis que pour
, tandis que pour
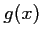 ,
, 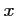 ne doit pas prendre de valeur telle que
ne doit pas prendre de valeur telle que 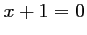 , soit
, soit
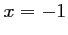 , et donc,
, et donc,
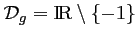
- 2)
Pour tout réel
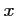 ,
,
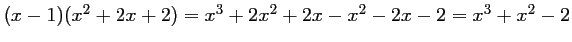 .
.
- 3)
Pour tout réel
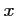 ,
,
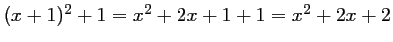 .
.
Pour tout nombre réel
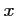 ,
,
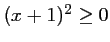 , et donc
, et donc
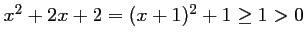 .
.
Ainsi,
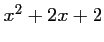 est toujours strictement positif.
est toujours strictement positif.
- 4)
Pour comparer les positions des courbes
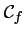 et
et
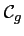 , on étudie le signe de
, on étudie le signe de 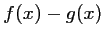 :
:
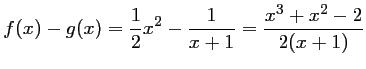
et donc, d'après la question 1),
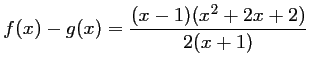 .
.
![$\displaystyle \begin{tabular}[t]{\vert c\vert ccccccc\vert}\hline
$x$&$-\infty...
...\mid$}& $-$\ & \mbox{$0\hspace{-0.67em}\mid$}& $+$\ & \\ \hline
\end{tabular} $](/Generateur-Devoirs/2nde/Chap5/ex3_c_img18.png)
Ainsi, 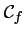 est au-dessus de
est au-dessus de
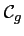 lorsque
lorsque
![$ x\in]-\infty;-1[\cup[1;+\infty[$](/Generateur-Devoirs/2nde/Chap5/ex3_c_img19.png) , et au-dessous lorsque
, et au-dessous lorsque
![$ x\in]-1;1]$](/Generateur-Devoirs/2nde/Chap5/ex3_c_img20.png) .
.
Les deux courbes se coupent en
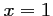 .
.
Cacher la correction
Voir aussi: