Ajustement affine par moindres carrés


Position du problème


On se donne deux séries de données: $X=(x_1,x_2,\dots,x_n)$ et $Y=(y_1,y_2,\dots,y_n)$ entre lesquelles on cherche un lien éventuel.

On peut représenter ces données graphiquement: c'est le nuage de points de coordonnées $M_i\lp x_i;y_i\rp$.
\[\psset{xunit=3cm,yunit=2cm,arrowsize=8pt} \begin{pspicture}(-.2,-0.2)(4.2,4.2) \psline{->}(-0.2,0)(4,0) \psline{->}(0,-0.2)(0,4) %\rput(1,2.){$\tm$} \psdots(.9,.52)(.92,1.2)(.92,.89)(.96,.6)(.97,.89)(.98,.89) \psdots(1,1)(1.1,1.2)(1.15,1.1)(1.2,1.35)(1.2,1.15)(1.17,1.) \psdots(1.3,1.3)(1.32,1.4)(1.35,1.41)(1.4,1.3)(1.43,1.37) \psdots(1.5,1.6)(1.55,1.7)(1.52,1.4)(1.6,1.6)(1.61,1.72)(1.65,1.4) \psdots(1.68,1.42)(1.7,2)(1.72,1.6)(1.76,1.7)(1.77,1.6)(1.78,1.75) \psdots(1.8,1.42)(1.82,2)(1.82,1.8)(1.86,1.7)(1.87,1.8)(1.88,1.99) \psdots(1.9,1.52)(1.92,2.2)(1.92,1.89)(1.96,1.6)(1.97,1.89)(1.98,1.89) \psdots(2,2)(2.1,2.2)(2.15,2.1)(2.2,2.35)(2.2,2.15)(2.17,2.)(2.18,1.8) \psdots(2.3,2.3)(2.32,2.4)(2.35,2.41)(2.4,2.3)(2.43,2.17) \psdots(2.5,2.6)(2.55,2.7)(2.52,2.4)(2.6,2.6)(2.61,2.72)(2.65,2.4) \psdots(2.68,2.42)(2.7,3)(2.72,2.6)(2.76,2.7)(2.77,2.6)(2.78,2.75) \psdots(2.8,2.42)(2.82,3)(2.82,2.8)(2.86,2.7)(2.87,2.8)(2.88,2.99) \psdots(2.9,2.52)(2.92,3.2)(2.92,2.89)(2.96,2.6)(2.97,2.89)(2.98,2.89) \psdots(1,1.6)(2,2.4)(1.5,1.1)(1.8,1.3)(2.2,1.7)(2.8,2.2) \end{pspicture}\]

Peut-on trouver, graphiquement dans ce nuage, et numériquement/algébriquement avec les données numériques des deux séries $X$ et $Y$, un lien entre ces séries.

L'ajustement affine consiste à cherhcer un tel lien sous une forme affine, c'est-à-dire sous la forme $Y=aX+b$, ou encore plus pécisément, pour tout $i$, $y_i=ax_i+b$.

Les questions principales sont:
  • comment déterminer les "meilleurs" coefficients 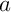$a$ et $b$

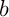
  • cet ajustement est-il pertinent ? permet-il de décrire "convenablement" les données ?

  • un ajustement par un autre type de fonction (exponentielle, logarithmique, parabolique, … ) est-il envisageable, et surtout est-il meilleur ?


On parle aussi de régression linéaire: un lien existe très certainement entre les données des séries $X$ et $Y$, mais ce lien peut être très complexe, au point de le rendre inaccessible.
L'ajustement affine permet de faire régresser cette complexité à celle d'un modèle ne contenant que deux paramètres. On fait régresser la complexité de notre situation de $2N$ paramètres, les données, à 2 paramètres, les coefficients $a$ et $b$.


Pour préciser les choses et construire cette "meilleure" régression affine, on considère un nombre plus faible de points, par exemple avec $n=6$ points (volontairement "très" espacés pour visualiser et comprendre plus aisément):
\[\psset{xunit=1.1cm,yunit=1.4cm,arrowsize=8pt} \begin{pspicture}(-.2,-.2)(7.2,5.4) \psline{->}(-0.1,0)(7,0) \psline{->}(0,-0.1)(0,5.2) \rput(1,2.){$\tm$}\rput(1,2.3){$M_1$} \rput(2,1){$\tm$}\rput(2,0.7){$M_2$} \rput(3,3.2){$\tm$}\rput(3,3.5){$M_3$} \rput(4,4){$\tm$}\rput(4,4.3){$M_4$} \rput(5,2.5){$\tm$}\rput(5,2.2){$M_5$} \end{pspicture}\]


On cherche alors à ajuster ce nuage de points par une droite. Il est clair que cet ajustement peut se faire de bien des manières, si on ne donne aucun critère particulier.
\[\psset{xunit=1.1cm,yunit=1.4cm,arrowsize=8pt} \begin{pspicture}(-1,-0.2)(7.6,5.6) \psline{->}(-0.2,0)(7,0) \psline{->}(0,-0.1)(0,5.2) \rput(1,2.){$\tm$}\rput(1,2.3){$M_1$} \rput(2,1){$\tm$}\rput(2,0.7){$M_2$} \rput(3,3.2){$\tm$}\rput(3,3.5){$M_3$} \rput(4,4){$\tm$}\rput(4,4.3){$M_4$} \rput(5,2.5){$\tm$}\rput(5,2.2){$M_5$} \psplot[linecolor=blue,linewidth=1.5pt]{-1}{7}{x 0.5 mul 1 add} \rput(6.9,4.6){\large\blue$D_2$} \psplot[linecolor=red,linewidth=1.5pt]{-1}{7}{x 0.4 mul 1.2 add} \rput(6.9,3.6){\large\red$D_3$} \psplot[linecolor=magenta,linewidth=1.5pt]{-.7}{7}{x 0.7 mul .3 add} \rput(6.9,5.4){\large\magenta$D_1$} \end{pspicture}\]

Quelle droite choisir ? Voir aussi cette animation interactive pour essayer d'en juger.

Moindres carrés


La méthode des moindres carrés permet de déterminer la meilleure droite parmi toutes les droites, "meilleure": le critère reste à définir.
Pour une droite candidate, à chaque point $M_i$ du nuage de points, on note $P_i$ sa projection sur la droite parallèlement à l'axe des ordonnées.

\[\psset{xunit=1.1cm,yunit=1.4cm,arrowsize=8pt} \begin{pspicture}(-1,-0.2)(7.4,5.4) \psline{->}(-0.2,0)(7,0) \psline{->}(0,-0.1)(0,5.2) % \rput(1,2.){$\tm$}\rput(1,2.3){$M_1$} \rput(1,1.2){$P_1$}\psline[linestyle=dashed](1,2)(1,1.5) % \rput(2,1){$\tm$}\rput(2,0.7){$M_2$} \rput(2,2.3){$P_2$}\psline[linestyle=dashed](2,1)(2,2) % \rput(3,3.2){$\tm$}\rput(3,3.5){$M_3$} \rput(3,2.2){$P_3$}\psline[linestyle=dashed](3,3.2)(3,2.5) % \rput(4,4){$\tm$}\rput(4,2.7){$P_4$} \rput(4,4.3){$M_4$}\psline[linestyle=dashed](4,4)(4,3) % \rput(5,2.5){$\tm$}\rput(5,2.2){$M_5$} \rput(5,3.8){$P_5$}\psline[linestyle=dashed](5,2.5)(5,3.5) % \psplot{-1}{7}{x 0.5 mul 1 add} \end{pspicture}\]


L'erreur commise en considérant le point $P_i$ au lieu du point $M_i$ est la distance $\varepsilon_i=M_iP_i$. On définit alors la distance entre la droite et le nuage de points par
\[d=\sum_{i=1}^n\varepsilon_i^2\]


Maintenant, en écrivant l'équation de la droite sous la forme $y=ax+b$ on a alors, $M_i\lp x_i;y_i\rp$ et $P_i\lp x_i;\widetilde{y_i}\rp$ avec, comme $P_i$ appartient à la droite, $\widetilde{y_i}=ax_i+b$, et la distance qui nous intéresse s'écrit:
\[\bgar{ll}d&=\dsp\sum_{i=1}^n\varepsilon_i^2 =\sum_{i=1}^n M_iP_i^2 \\[1.2em] &=\dsp\sum_{i=1}^n \lp y_i-\widetilde{y_i}\rp^2\enar\]


Le problème se formue maintenant plus précisément: déterminer les coefficients $a$ et $b$ de l'équation $y=ax+b$ de la droite qui minimisent la distance $d$ précédente.
La droite ainsi trouvée (car il y en a une et une seule comme nous allons le voir et le démontrer par la suite) s'appelle alors droite d'ajustement par la méthode des moindres carrés ou encore droite de régression affine par la méthode des moindres carrés, ou plus familièrement droite des moindres carrés.

On entend parfois aussi "régression linéaire" (comme sur les calculatrices), qui est un abus de langage, la droite recherchée ne passe pas a priori par l'origine,et sont expression n'a donc pas de raison particulière d'être linéaire, mais du moins affine…

Calcul des coeffficients


On peut proposer diverses approches pour montrer l'existence et l'unicité de ces coefficients et en donner des formules de calcul.
Le problème est, pour préciser les choses: déterminer $a$ et $b$ tels que
\[d(a,b)=\sum_{i=1}^n\lp y_i-\widetilde{y_i}\rp^2\]

où $\widetilde{y_i}=ax_i+b$, soit minimal.

Démonstration rapide


Une démonstration un peu rapide, et qui peut se faire dès le lycée car ne nécessitant de connaissances que sur le second degré, consiste à admettre tout d'abord que, comme au mieux on aimerait avoir $y_i=ax_i+b$, en moyenne on a $\overline{y}=a\overline{x}+b$: la droite passe par le point moyen $G\lp\overline{x};\overline{y}\rp$.
Ceci étant admis, on a alors $b=\overline{y}-a\overline{x}$ et la distance à minimiser ne dépend plus que d'un paramètre
\[\bgar{ll}d(a,b)&=\dsp\sum_{i=1}^n\lp y_i-\widehat{y_i}\rp^2\\[1.2em] &=\dsp\sum_{i=1}^n\Bigl( y_i-\lp ax_i+b\rp\Bigr)^2\\[1.2em] &=\dsp\sum_{i=1}^n\Bigl( y_i-\lp ax_i+\overline{y}-a\overline{x}\rp\Bigr)^2\\[1.2em] &=\dsp\sum_{i=1}^n\Bigl( a\lp\overline{x}-x_i\rp-\lp\overline{y}-y_i\rp\Bigr)^2 \enar\]

et donc, en développant l'identité remarquable:
\[\bgar{ll}d(a,b)&=\dsp\sum_{i=1}^n a^2\lp\overline{x}-x_i\rp -2a\lp\overline{x}-x_i\rp\lp\overline{y}-y_i\rp +\lp\overline{y}-y_i\rp^2\\[1.2em] &=\dsp a^2\sum_{i=1}^n\lp\overline{x}-x_i\rp -2a\sum_{i=1}^n\lp\overline{x}-x_i\rp\lp\overline{y}-y_i\rp +\sum_{i=1}^n\lp\overline{y}-y_i\rp^2 \enar\]

Cette expression est celle d'un trinôme du second degré en la variable 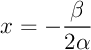$a$ qu'on cherche. Comme on sait que le trinôme du second degré $\alpha x^2+\beta x+\gamma$ admet son extremum en $x=-\dfrac{\beta}{2\alpha}$, on trouve ici que le minimum recherché est atteint lorsque
\[\bgar{ll}a&=-\dfrac{\dsp-2\sum_{i=1}^n\lp\overline{x}-x_i\rp\lp\overline{y}-y_i\rp}{\dsp2\sum_{i=1}^n\lp\overline{x}-x_i\rp}\\[2.5em] &=\dfrac{\dsp\sum_{i=1}^n\lp\overline{x}-x_i\rp\lp\overline{y}-y_i\rp}{\dsp\sum_{i=1}^n\lp\overline{x}-x_i\rp}\enar\]



Démonstration complète analytique: minimum d'une fonction de deux variables


Plus rigoureusement, sans admettre l'expression de $b$ (qu'on va retrouver), on est face à une fonction de deux variables
\[d(a,b)=\sum_{i=1}^n\Bigl( y_i-ax_i-b\Bigr)^2\]

dont on cherche le minimum.
Ce minimum est à chercher parmi les points critiques, c'est-à-dire où les dérivées partielles s'annulent:
\[\la\bgar{ll} \dfrac{\partial d(a,b)}{\partial a}= -2\dsp\sum_{i=1}^n x_i \Bigl( y_i-ax_i-b\Bigr) =0 \\[1.5em] \dfrac{\partial d(a,b)}{\partial b}= -2\dsp\sum_{i=1}^n \Bigl( y_i-ax_i-b\Bigr) =0 \enar\right.\]

La deuxième équation se réécrit, en séparant les sommes,
\[\sum_{i=1}^n y_i-a\sum_{i=1}^nx_i-b\sum_{i=1}^n1=0\]

soit, en divisant par $n$,
\[\overline{y}-a\overline{x}-b=0 \iff \overline{y}=a\overline{x}+b\]

et on retrouve la propriété admise dans la section précédente.

Maintenant, l'annulation de la première dérivée partielle donne
\[\sum_{i=1}^nx_iy_i-a\sum_{i=1}^nx_i^2-b\sum_{i=1}^nx_i=0\]

soit, avec $b=\overline{y}-a\overline{x}$,
\[\sum_{i=1}^nx_iy_i-a\sum_{i=1}^nx_i^2-\lp\overline{y}-a\overline{x}\rp\sum_{i=1}^nx_i=0\]

donc

\[a=\dfrac{\dsp b\sum_{i=1}^nx_i-\sum_{i=1}^nx_iy_i}{\dsp\sum_{i=1}^nx_i^2}\]


Il reste alors à vérifier si ce point critique est bien un minimum. Cette information nous est donnée par la matrice Hessienne:
\[\bgar{ll}H(a,b)&=\lp\bgar{cc} \dfrac{\partial^2d(a,b)}{\partial a^2} & \dfrac{\partial^2d(a,b)}{\partial a\partial b}\\[1em] \dfrac{\partial^2d(a,b)}{\partial a\partial b} & \dfrac{\partial^2d(a,b)}{\partial b^2} \enar\rp\\[3em] &=\lp\bgar{cc} 2\dsp\sum_{i=1}^n x_i^2 & 2\dsp\sum_{i=1}^n x_i \\[1em] 2\dsp\sum_{i=1}^n x_i & 2n \enar\rp \enar\]

On a alors
\[\bgar{ll} \det\lp H(a,b)\rp&=\dsp4n\sum_{i=1}^n x_i^2-4\lp\sum_{i=1}^nx_i\rp^2\\[1.6em] &=4n^2\text{Var}(X)>0\enar \]

ce qui montre qu'on est bien face à un extremum local, et, comme
\[\text{Tr}\lp H(a,b)\rp=2\sum_{i=1}^n x_i^2+2n>0\]

il s'agit bien d'un minimum.

Interprétation matricielle: système d'équations surdéterminé et système normal


Admettons qu'on cherche l'équation d'une droite qui passe exatement par tous les points $M_i\lp x_i;y_i\rp$, c'est-à-dire que, pour tout entier $i$, $y_i=ax_i+b$ ou encore, on cherche $a$ et $b$ solutions du système linéaire
\[\la\bgar{lcl} a x_1+b=&y_1 \\ a x_2+b=&y_2 \\ \dots \\ a x_n+b=&y_n\enar\right.\]

ou encore, matriciellement, on cherche $U=\lp\bgar{c}a\\b\enar\rp$ tel que $AU=Y$ avec
\[A=\lp\bgar{cc}x_1 & 1\\x_2&1\\\dots\\x_n&1\enar\rp\]

et le second membre
\[Y=\lp\bgar{c}y_1\\y_2\\\dots\\y_n\enar\rp\]

Ce système est clairement surdimensionné, ou surdéterminé: il y a beaucoup plus d'équations que d'inconnues et on s'attend donc tout aussi clairement à ce qu'il n'y ait pas de solution (tout autant à ce que, géométrique, tous les points du nuages ne soient pas alignés).

Par contre, on peut néanmoins chercher le vecteur $U$ qui est "le plus proche de résoudre ce système", c'est-à-dire le nouveau problème:
Chercher $U$ tel que $\left\|Y-AU\right\|$ soit minimal.
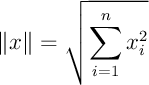On prend ici la norme euclidienne: si $x=\lp x_1, x_2, \dots, x_n\rp$, alors $\dsp\left\| x\right\|=\sqrt{\sum_{i=1}^nx_i^2}$.


Les équations donnant le point critique trouvé précédemment s'écrivent
\[\bgar{ll} \la\bgar{ll} \dfrac{\partial d(a,b)}{\partial a}=0 \\[1.5em] \dfrac{\partial d(a,b)}{\partial b}=0 \enar\right. \iff \la\bgar{ll}\dsp\sum_{i=1}^n x_i \Bigl( y_i-ax_i-b\Bigr) =0\\[1.5em] \dsp\sum_{i=1}^n \Bigl( y_i-ax_i-b\Bigr) =0 \enar\right. \\[3.5em] \iff \la\bgar{ll} \dsp a\sum_{i=1}^nx_i^2+b\sum_{i=1}^nx_i=\sum_{i=1}^nx_iy_i \\[1.5em] \dsp a\sum_{i=1}^nx_i+nb=\sum_{i=1}^ny_i \enar\right. \\[3.5em] \iff ^tAAU=\,^tAY \enar \]

car
\[^tAA= \lp\bgar{cccc}x_1&x_2&\dots&x_n\\1&1&\dots&1\enar\rp\, \lp\bgar{cc}x_1&1\\x_2&1\\\dots\\x_n&1\enar\rp =\lp\bgar{cc}\sum x_i^2 & \sum x_i\\[.6em]\sum x_i & n\enar\rp\]


Ce dernier système est un système linéaire 2x2, appelé le système d'équations normales.

On peut retenir, d'une manière plus générale que, si $AU=Y$ est un système linéaire surdimensionné, alors en multipliant par la transposée de la matrice du système:
\[^tAAU=\,^tAY\]

est un système dont la solution $\widetilde{U}$ est la meilleure, c'est-à-dire ici qui minimise
\[\left\|Y-AU\right\|^2\]

parmi tous les $U$ possible, et avec $\left\|\,.\,\right\|$ désignant la norme euclidienne.

Remarque: on appelle matrice normale toute matrice $M$ qui vérifie $^tM=M$.
Ici, la matrice du système d'équations normales et $M=\,^tAA$, qui vérifie bien cette propriété, d'où le nom donné à ce système d'équations.


On peut démontrer ce résultat exclusivement algébriquement dans un espace euclidien réel.

Propriété: Soit $A$ et $Y$ donnés et $\widetilde{U}$ tel que $^tAA\widetilde{U}=\,^tAY$ alors
\[\text{Min}\Bigl\{\left\|AU-Y\right\|\,,U\in\R^n\Bigr\} =\left\|A\widetilde{U}-Y\right\|\]

$\widetilde{U}$ est de plus unique.


Démonstration: Soit $h\in\R^n$ quelconque, alors en notant $(u,v)$ le produit scalaire euclidient,
\[\bgar{ll} \left\|Y-A\lp\widetilde{U}+h\rp\right\|^2 &=\Bigl( Y-A\lp\widetilde{U}+h\rp,Y-A\lp\widetilde{U}+h\rp\Bigr)\\[1.5em] &=\Bigl( \lp Y-A\widetilde{U}\rp-Ah,\lp Y-A\widetilde{U}\rp-Ah\Bigr)\\[1.5em] &=\left\|Y-A\widetilde{U}\right\|^2 -2\Bigl(\lp Y-A\widetilde{U}\rp,Ah\Bigr) +\left\|Ah\right\|^2\\[1.4em] &=\left\|Y-A\widetilde{U}\right\|^2 -2\Bigl(\,^tA\lp Y-A\widetilde{U}\rp,h\Bigr) +\left\|Ah\right\|^2\\[1.4em] &=\left\|Y-A\widetilde{U}\right\|^2 -2\Bigl(\underbrace{\,^tAY-\,^tAA\widetilde{U}}_{=0},h\Bigr) +\left\|Ah\right\|^2\\[1.4em] \enar\]

Ainsi, pour tout vecteur $h$,
\[\left\|Y-A\lp\widetilde{U}+h\rp\right\|^2 =\left\|Y-A\widetilde{U}\right\|^2+\left\|Ah\right\|^2 \geqslant\left\|Y-A\widetilde{U}\right\|^2\]

ce qui montre que $\left\|Y-A\widetilde{U}\right\|$ est bien le minimum.

Enfin, $\widetilde{u}$ est unique car solution de $^tAAU=\,^tAY$ et que
\[\bgar{ll}\det\lp\,^tAA\rp&=\left|\bgar{cc}\sum x_i^2 & \sum x_i\\[.6em]\sum x_i & n\enar\right|\\[1.8em] &=n\sum x_i^2-\lp\sum x_i\rp^2\\[.8em] &=n^2\lp \dfrac1n\sum x_i^2-\lp\dfrac1n\sum x_i\rp^2\rp\\[1.4em] &=n^2\text{Var}(X)>0\enar\]


Lien
LongPage: h2: 4 - h3: 2