Devoir corrigé de maths en Terminale générale, spécialité mathématiques
Annale Bac, spé maths - 11 mai 2022
Baccalauréat 11 mai 2022. Sujet posé en spécialité mathématiques, filière générale. Correction détaillée du sujet.Exercice 1: Exponentielle et suite récurrente
Dans le cadre d'un essai clinique on envisage deux protocoles de traiterment de
d'une maladie.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction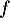 définie sur l'intervalle [0 ; 10] par
définie sur l'intervalle [0 ; 10] par
![\[f(t) = 3t e^{-0,5t+1},\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022/2.png)
où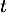 désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
désigne le temps, exprimé en heure, écoulé depuis la prise du comprimé.
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de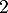 mg de médicament puis à réinjecter toutes les heures une dose de
mg de médicament puis à réinjecter toutes les heures une dose de  mg.
mg.
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite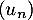 où, pour tout entier naturel
où, pour tout entier naturel 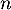 ,
, 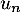 désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la
désigne la quantité de médicament, exprimée en mg, présente dans le sang du patient immédiatement après l'injection de la 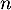 -ième heure. On a donc
-ième heure. On a donc 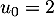 .
.
L'objectif de cet exercice est d'étudier, pour ces deux protocoles, l'évolution de la quantité de médicament présente dans le sang d'un patient en fonction du temps.
Les parties A et B sont indépendantes
Partie A : Étude du premier protocole
Le premier protocole consiste à faire absorber un médicament, sous forme de comprimé, au patient.
On modélise la quantité de médicament présente dans le sang du patient, exprimée en mg, par la fonction
où
-
- On admet que la fonction
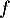 est dérivable sur l'intervalle [0 ; 10] et on note
est dérivable sur l'intervalle [0 ; 10] et on note 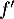 sa fonction dérivée.
Montrer que, pour tout nombre réel
sa fonction dérivée.
Montrer que, pour tout nombre réel 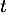 de [0 ; 10], on a:
de [0 ; 10], on a: 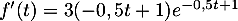 .
.
- En déduire le tableau de variations de la fonction
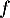 sur l'intervalle [0 ; 10].
sur l'intervalle [0 ; 10].
- Selon cette modélisation, au bout de combien de temps la quantité de médicament présente dans le sang du patient sera-t-elle maximale ? Quelle est alors cette quantité maximale?
- On admet que la fonction
-
- Montrer que l'équation
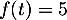 admet une unique solution sur l'intervalle [0 ; 2] notée
admet une unique solution sur l'intervalle [0 ; 2] notée 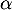 , dont on donnera une valeur approchée à
, dont on donnera une valeur approchée à 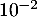 près.
On admet que l'équation
près.
On admet que l'équation 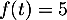 admet une unique solution sur l'intervalle [2 ; 10], notée
admet une unique solution sur l'intervalle [2 ; 10], notée 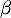 , et qu'une valeur approchée de
, et qu'une valeur approchée de 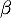 à
à 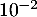 près est 3,46.
près est 3,46.
- On considère que ce traitement est efficace lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5 mg. Déterminer, à la minute près, la durée d'efficacité du médicament dans le cas de ce protocole.
- Montrer que l'équation
Partie B : Étude du deuxième protocole
Le deuxième protocole consiste à injecter initialement au patient, par piqüre intraveineuse, une dose de
On suppose que le médicament se diffuse instantanément dans le sang et qu'il est ensuite progressivement éliminé.
On estime que lorsqu'une heure s'est écoulée après une injection, la quantité de médicament dans le sang a diminué de 30 % par rapport à la quantité présente immédiatement après cette injection.
On modélise cette situation à l'aide de la suite
- Calculer, selon cette modélisation, la quantité
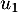 , de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
, de médicament (en mg) présente dans le sang du patient immédiatement après l'injection de la première heure.
- Justifier que, pour tout entier naturel
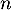 , on a :
, on a : 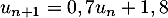 .
.
-
- Montrer par récurrence que, pour tout entier naturel
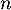 , on a :
, on a : 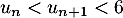 .
.
- En déduire que la suite
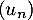 est convergente. On note
est convergente. On note 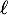 sa limite.
sa limite.
- Déterminer la valeur de
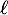 . Interpréter cette valeur dans le contexte de l'exercice.
. Interpréter cette valeur dans le contexte de l'exercice.
- Montrer par récurrence que, pour tout entier naturel
- On considère la suite
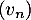 définie, pour tout entier naturel
définie, pour tout entier naturel 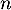 , par
, par 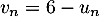 .
.
- Montrer que la suite
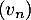 est une suite géométrique de raison
est une suite géométrique de raison 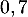 dont on précisera le premier terme.
dont on précisera le premier terme.
- Déterminer l'expression de
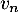 en fonction de
en fonction de 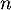 , puis de
, puis de 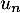 n en fonction de
n en fonction de 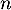 .
.
- Avec ce protocole, on arrête les injections lorsque la quantité de médicament présente dans le sang du patient est supérieure ou égale à 5,5 mg. Déterminer, en détaillant les calculs, le nombre d'injections réalisées en appliquant ce protocole.
- Montrer que la suite
Correction exercice 1
Partie A : Étude du premier protocole
Partie B : Étude du deuxième protocole
Cacher la correction
Partie A : Étude du premier protocole
-
- On a
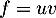 avec
avec 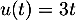 donc
donc 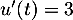 et
et 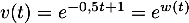 avec
avec
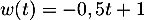 donc
donc 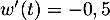 et alors
et alors 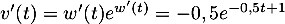 .
.
On obtient alors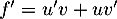 , soit
, soit
![\[\begin{array}{ll}f'(t)&=3e^{-0,5t+1}+3t\tm\lp-0,5e^{-0,5t+1}\rp\\[.4em]
&=3e^{-0,5t+1}\lp1-0,5t\rp\\[.4em]
&=3(-0,5t + 1)e^{-0,5t+1}\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/9.png)
- On a alors le signe de lé dérivée et le sens de variation:
![\[\begin{tabular}{|c|*5c|}\hline
$t$ & 0 && 2 && 10 \\\hline
$-0,5t+1$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
$e^{-0,5t+1}$ && $+$ &\vline & $+$ & \\\hline
$f'(t)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ & \\\hline
&&&&&\\
$f$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/10.png)
- Selon cette modélisation, la quantité maximale de médicament présente dans le sang du patient sera de
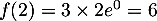 mg, au bout de 2 heures.
mg, au bout de 2 heures.
- On a
-
- Sur [0;2], la fonction
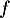 est continue (car même dérivable),
strictement croissante, avec
est continue (car même dérivable),
strictement croissante, avec 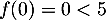 et
et 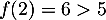 ,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution
,
et ainsi, d'après le théorème des valeurs intermédiaires
(théorème de la bijection), on sait donc qu'il existe une unique
solution 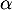 à l'équation
à l'équation 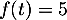 .
.
Avec la calculatrice, par balayage par exemple, on touve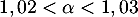 soit,
soit, 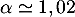 .
.
- On peut compléter le tableau de variation:
![\[\begin{tabular}{|c|*9c|}\hline
$t$ & 0 &&$\alpha$ && 2 &&$\beta$&& 10 \\\hline
&&&&&&&&&\\
$f$&&\psline[arrowsize=8pt]{->}(-.5,-.5)(1.3,.5)&5&&&
\psline[arrowsize=8pt]{->}(-.2,.5)(1.4,-.5)&5&&\\
&&&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/19.png)
grâce auquel on trouve que la durée d'efficacité du médicament est donc de soit 2,44 heures, ou encore 2 heures et 26 minutes.
soit 2,44 heures, ou encore 2 heures et 26 minutes.
- Sur [0;2], la fonction
Partie B : Étude du deuxième protocole
- Selon cette modélisation, à la première heure la quantité dans le sang a diminué de 30%, il en reste donc
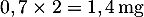 .
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
.
On réinjecte de plus une nouvelle dose de 1,8 mg, et on trouve donc que
![\[u_1=0,7\tm2+1,8=3,2\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/22.png)
- De même que précédemment, à la (n+1)-ème heure,
la quantité dans le sang présente l'heure précédente, soit
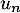 a diminué de 30%, soit
a diminué de 30%, soit 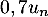 , et on réinjecte, donc ajoute, 1,8 mg.
, et on réinjecte, donc ajoute, 1,8 mg.
On obtient donc bien la relation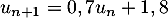 .
.
-
- Soit la proposition
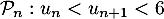 .
.
Initialisation: on a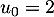 et
et 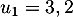 d'où
d'où
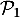 est vraie:
est vraie: 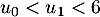 .
.
Hérédité: Supposons que pour un certain entier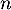 ,
,
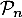 soit vraie, c'est-à-dire
soit vraie, c'est-à-dire
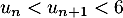 .
.
Alors, en multipliant par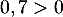 , on obtient
, on obtient
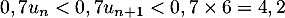 ,
,
puis en ajoutant 1,8 on aboutit à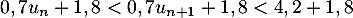 ,
,
c'est-à-dire exactement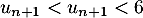 et qui montre donc
et qui montre donc 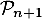 est alors vraie.
est alors vraie.
Conclusion: on vient donc de démontrer, d'après le principe de récurrence, que pour tout entier ,
,
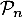 est vraie, c'est-à-dire
est vraie, c'est-à-dire 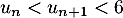 .
.
- On déduit du résultat précédent que la suite
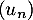 est croissante et aussi qu'elle est majorée par 6.
est croissante et aussi qu'elle est majorée par 6.
On en déduit donc (théorème de convergence monotone) qu'elle converge vers une limite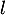 .
.
- On a
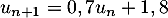 et on sait que
et on sait que  .
.
Ainsi, on doit nécessairement avoir (théorème du point fixe), que
![\[l=0,7l+1,8\iff l=\dfrac{1,8}{0,3}=6\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/46.png)
- Soit la proposition
-
- Pour tout entier
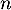 , on a
, on a
![\[\begin{array}{ll}v_{n+1}&=6-u_{n+1}\\
&=6-\lp0,7u_n+1,8\rp\\
&=4,2-0,7u_n\\
&=0,7\lp6-u_n\right)
=0,7v_n\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/48.png)
ce qui montre que la suite est bien géométrique de raison
est bien géométrique de raison 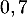 et de premier terme
et de premier terme 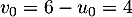 .
.
- On en déduit alors que, pour tout entier
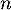 ,
,
![\[v_n=v_0\times q^n=4\times0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/53.png)
puis, comme , que
, que
![\[u_n=6-4\tm0,7^n\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/55.png)
- On arrête les injections lorsque la quantité de médicament
présente dans le sang du patient est supérieure ou égale à 5,5 mg,
soit lorsque
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&6-4\tm0,7^n\geqslant5,5\\
\iff&-4\tm0,7^n\geqslant-0,5\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/56.png)
soit, en divisant par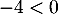 , puis en prenant le logarithme népérien qui est strictement croissant,
, puis en prenant le logarithme népérien qui est strictement croissant,
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff&0,7^n\leqslant\dfrac{-0,5}{-4}=0,125\\
\iff&\ln\lp0,7^n\rp=n\ln(0,7)\leqslant\ln(0,125)\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/58.png)
Enfin, en divisant par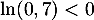 , on obtient finalement
, on obtient finalement
![\[\begin{array}{ll}&u_n\geqslant5,5\\
\iff n\geqslant\dfrac{\ln(0,125)}{\ln(0,7)}\simeq5,8\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex11052022_c/60.png)
Comme on réalise une injection par heure, il faut donc en réaliser 6.
- Pour tout entier
Cacher la correction
Exercice 2: Un peu de tout dans l'espace
Dans l'espace rapporté à un repère orthonormé 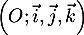 ,
on considère:
,
on considère:
- le point A de coordonnées
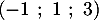 ,
, - la droite
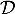 dont une représentation paramétrique est:
dont une représentation paramétrique est:
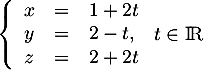 .
.
-
- Donner les coordonnées d'un vecteur directeur
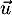 de la droite
de la droite 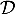 .
On admet que le point A n'appartient pas à la droite
.
On admet que le point A n'appartient pas à la droite 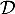 .
.
- Montrer que le point
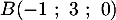 appartient à la droite
appartient à la droite 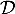 .
.
- Calculer le produit scalaire
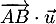 .
.
- Donner les coordonnées d'un vecteur directeur
- On note
 le plan passant par le point A et orthogonal à la droite
le plan passant par le point A et orthogonal à la droite 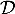 , et on appelle H le point d'intersection du plan
, et on appelle H le point d'intersection du plan 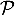 et de la droite
et de la droite 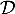 . Ainsi, H est le projeté orthogonal de A sur la droite
. Ainsi, H est le projeté orthogonal de A sur la droite 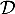 .
.
- Montrer que le plan
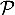 admet pour équation cartésienne:
admet pour équation cartésienne: 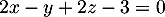 .
.
- En déduire que le point H a pour coordonnées
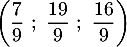 .
.
- Calculer la longueur AH. On donnera une valeur exacte.
- Montrer que le plan
- Dans cette question, on se propose de retrouver les coordonnées du point H, projeté orthogonal du point A sur la droite
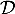 , par une autre méthode.
On rappelle que le point B
, par une autre méthode.
On rappelle que le point B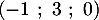 appartient à la droite
appartient à la droite 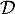 et que le vecteur
et que le vecteur 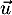 est un vecteur directeur de la droite
est un vecteur directeur de la droite 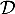 .
.
- Justifier qu'il existe un nombre réel
 tel que
tel que 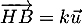 .
.
- Montrer que
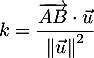 .
.
- Calculer la valeur du nombre réel
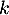 et retrouver les coordonnées du point H.
et retrouver les coordonnées du point H.
- Justifier qu'il existe un nombre réel
- On considère un point C appartenant au plan
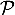 tel que le volume du tétraèdre ABCH soit égal à
tel que le volume du tétraèdre ABCH soit égal à  .
Calculer l'aire du triangle ACH.
.
Calculer l'aire du triangle ACH.
On rappelle que le volume d'un tétraèdre est donné par: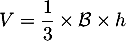 où
où  désigne l'aire d'une base
et
désigne l'aire d'une base
et 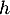 la hauteur relative à cette base.
la hauteur relative à cette base.
Correction exercice 2
Cacher la correction
-
- Un vecteur directeur est donné par
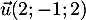
- Avec les coordonnées de B, on a
![\[\la\begin{array}{lcl}
-1&=&1+2t\\3 &=& 2 - t,\\0&=& 2+2t
\enar\right.
\iff
\la\begin{array}{lcl}
t&=&-1\\t&=&-1,\\t&=&-1
\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/2.png)
ce qui montre que B appartient bien à la droite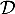 .
.
- On a
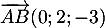 donc
donc
![\[\overrightarrow{AB}\cdot\vec{u}=0\tm2+2\tm(-1)+(-3)\tm2=-8\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/5.png)
- Un vecteur directeur est donné par
-
(4,0)
\psline(4,0)(4,-2)
\rput(4,1){$\tm$}\rput(4.3,1.2){$H$}
\rput(3.7,3.5){$\mathcal{D}$}
\psline[linecolor=blue,linewidth=2pt]{->}(4,-1.5)(4,-.5)
\psline[linecolor=blue](3.92,-1.5)(4.08,-1.5)
\rput(4.25,-1.1){\blue$\vec{u}$}
\rput(4,2.6){$\tm$}\rput(4.3,2.7){$B$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/6.png)
- Le plan
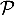 est orthogonale à la droite
est orthogonale à la droite 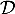 dirigée par
dirigée par
 qui est donc un vecteur normal à ce plan qui admet
donc une équation cartésienne de la forme
qui est donc un vecteur normal à ce plan qui admet
donc une équation cartésienne de la forme
![\[2x-y+2z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/10.png)
On sait de plus que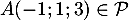 , et donc que
, et donc que
![\[2(-1)-(1)+2(3)+d=0\iff d=-3\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/12.png)
Finalement, on a trouvé une équation cartésienne du plan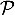 :
:
![\[\mathcal{P}: 2x - y + 2z - 3 = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/14.png)
- Le plan
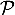 et la droite
et la droite 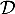 sont orthogonaux;
en particulier ils se coupent en un unique point
sont orthogonaux;
en particulier ils se coupent en un unique point 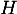 .
.
Soit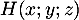 , alors
, alors
![\[H\in\mathcal{D}\iff
\la\begin{array}{lcl}
x&=&1+2t\\y &=& 2 - t,\\z&=& 2+2t
\enar\right. t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/19.png)
et de plus,
![\[\begin{array}{ll}H\in\mathcal{P}&\iff 2x - y + 2z - 3 = 0\\
&\iff2(1+2t)-(2-t)+2(2+2t)-3=0\\
&\iff t=-\dfrac19
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/20.png)
et on obtient alors les coordonnées
![\[\la\begin{array}{lcl}
x&=&1+2\tm\lp-1\frac19\rp=\frac79\\[.4em]
y &=& 2 - \lp-\frac19\rp=\frac{19}9\\[.4em]
z&=& 2+2\lp-\frac19\rp=\frac{16}9
\enar\right. t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/21.png)
qui sont bien les coordonnées recherchées du point H.
-
![\[\begin{array}{ll}
AH&=\sqrt{\lp\dfrac79-(-1)\rp^2+\lp\dfrac{19}9-1\rp^2+\lp\dfrac{16}9-3\rp^2}\\
&=\sqrt{\dfrac{16^2+10^2+11^2}{9^2}}
=\dfrac{\sqrt{253}}9
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/22.png)
- Le plan
-
- Les points H et B appartiennent tous les deux à la droite
 ,
et
,
et  est un vecteur directeur de cette droite.
est un vecteur directeur de cette droite.
On en déduit que les vecteurs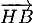 et
et 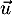 sont colinéaires,
c'est-à-dire qu'il existe un réel
sont colinéaires,
c'est-à-dire qu'il existe un réel 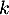 tel que
tel que
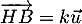 .
.
- D'après le résultat précédent, en prenant le produit scalaire
avec
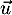 on obtient
on obtient
![\[\overrightarrow{HB}=k\vec{u}\implies \overrightarrow{HB}\cdot\vec{u}=k\vec{u}\cdot\vec{u}=\left\|\vec{u}\right\|^2\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/30.png)
d'où
![\[k=\dfrac{\overrightarrow{HB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/31.png)
Maintenant pour faire intervenir le vecteur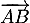 on peut utiliser la
relation de Chasles:
on peut utiliser la
relation de Chasles:
![\[\overrightarrow{HB}=\overrightarrow{HA}+\overrightarrow{AB}
\implies
\overrightarrow{HB}\cdot\vec{n}=\overrightarrow{HA}\cdot\vec{n}+\overrightarrow{AB}\cdot\vec{n}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/33.png)
or car
car 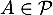 et
et 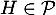 et
et 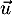 normal à
normal à 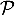 .
.
On vient donc de trouver que
![\[\overrightarrow{HB}\cdot\vec{n}=\overrightarrow{AB}\cdot\vec{n}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/39.png)
et donc la relation souhaitée:
![\[k=\dfrac{\overrightarrow{HB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}
=\dfrac{\overrightarrow{AB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/40.png)
-
D'après la question 1.c. on a
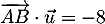 ,
et comme
,
et comme 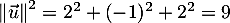 , on obtient
que
, on obtient
que
![\[k=\dfrac{-8}9\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/43.png)
et on retrouve les coordonnées du point H(x;y;z):
![\[\overrightarrow{HB}=k\vec{u}
\iff
\la\begin{array}{lcl}
-1-x&=&-\dfrac89\tm2\\
3-y&=&-\dfrac89\tm(-1)\\
0-z&=&-\dfrac89\tm2
\enar\right.
\iff
\la\begin{array}{lcl}
x&=&-1+\dfrac{16}9=\dfrac79\\
y&=&3-\dfrac89=\dfrac{19}9\\
z&=&\dfrac{16}9
\enar\right.
\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/44.png)
- Les points H et B appartiennent tous les deux à la droite
- BH est une hauteur relative à la base ACH,
et donc, avec
![\[V = \dfrac13 \times \mathcal{B} \times h\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/45.png)
avec
![\[\begin{array}{ll}
h&=BH=\sqrt{\lp\dfrac79-(-1)\rp^2+\lp\dfrac{19}9-3\rp^2+\lp\dfrac{16}9-0\rp^2}\\
&=\sqrt{\dfrac{16^2+8^2+16^2}{9^2}}
=\dfrac{8}{9}\sqrt{9}=\dfrac{24}9
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/46.png)
et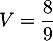 ,
d'où l'aire de la base ACH:
,
d'où l'aire de la base ACH:
![\[\dfrac89=\dfrac13\tm\mathcal{B}\tm\dfrac{24}{9}
\iff
\mathcal{B}=1\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/48.png)
Cacher la correction
Exercice 3: Arbre, loi binomiale et python
Le directeur d'une grande entreprise a proposé à l'ensemble de ses salariés un stage de formation à l'utilisation d'un nouveau logiciel.
Ce stage a été suivi par 25 % des salariés.
Ce stage a été suivi par 25 % des salariés.
- Dans cette entreprise, 52 % des salariés sont des femmes, parmi lesquelles
40 % ont suivi le stage.
On interroge au hasard un salarié de l'entreprise et on considère les évènements: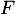 : « le salarié interrogé est une femme »,
: « le salarié interrogé est une femme »,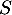 : « le salarié interrogé a suivi le stage ».
: « le salarié interrogé a suivi le stage ».
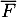 et
et 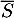 désignent respectivement les évènements contraires des évènements
désignent respectivement les évènements contraires des évènements 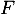 et
et  .
.
- Donner la probabilité de l'évènement

- Recopier et compléter les pointillés de l'arbre pondéré ci-contre sur
les quatre branches indiquées.
- Démontrer que la probabilité que la personne interrogée soit une femme ayant suivi le stage est égale à
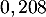 .
.
- On sait que la personne interrogée a suivi le stage. Quelle est la probabilité que ce soit une femme ?
- Le directeur affirme que, parmi les hommes salariés de l'entreprise, moins de 10 % ont suivi le stage. Justifier l'affirmation du directeur.
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$F$}
\rput(.8,.9){\dots}
\rput(.8,-1){\dots}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{F}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$S$}
\rput(2.8,1.7){\dots}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{S}$}
\rput(2.8,.2){\dots}
%\rput(2.8,-.4){}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{S}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$S$}
%\rput(2.8,-1.8){}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022/11.png)
- On note
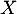 la variable aléatoire qui à un échantillon de
la variable aléatoire qui à un échantillon de 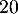 salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
- Déterminer, en justifiant, la loi de probabilité suivie par la variable aléatoire X,
- Déterminer, à
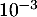 près, la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
près, la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
- Le programme ci-dessous, écrit en langage Python, utilise la fonction binomiale
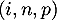 créée pour l'occasion qui renvoie
la valeur de la probabilité
créée pour l'occasion qui renvoie
la valeur de la probabilité 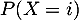 dans le cas où la variable aléatoire
dans le cas où la variable aléatoire 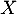 suit une loi binomiale de paramètres
suit une loi binomiale de paramètres 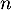 et
et 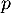 .
.
![\[\fbox{\begin{minipage}{7cm}
def proba(k):\\
\hspace*{2em} P=0\\
\hspace*{2em} for i in range(0,k+1) :\\
\hspace*{4em} P=P+binomiale(i,20,0.25)\\
\hspace*{2em} return P
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022/20.png)
Déterminer, à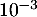 près, la valeur renvoyée par ce programme lorsque l'on saisit proba(5) dans la console Python.
Interpréter cette valeur dans le contexte de l'exercice.
près, la valeur renvoyée par ce programme lorsque l'on saisit proba(5) dans la console Python.
Interpréter cette valeur dans le contexte de l'exercice.
- Déterminer, à
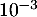 près, la probabilité qu'au moins 6 salariés dans un échantillon de 0 aient suivi le stage.
près, la probabilité qu'au moins 6 salariés dans un échantillon de 0 aient suivi le stage.
- Cette question est indépendante des questions 1 et 2.
Pour inciter les salariés à suivre le stage, l'entreprise avait décidé d'augmenter les salaires des salariés ayant suivi le stage de 5 %, contre 2 % d'augmentation pour les salariés n'ayant pas suivi le stage. Quel est le pourcentage moyen d'augmentation des salaires de cette entreprise dans ces conditions ?
Correction exercice 3
Cacher la correction
-
- D'après l'énoncé, on a
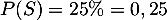 .
.
-
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$F$}
\rput(.8,.9){52\%}
\rput(.8,-1){48\%}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{F}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$S$}
\rput(2.8,1.7){40\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{S}$}
\rput(2.8,.2){60\%}
%\rput(2.8,-.4){}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{S}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$S$}
%\rput(2.8,-1.8){}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/2.png)
- On cherche la probablité
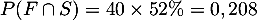 .
.
- La probabilité que ce soit une femme, sachant qu'elle a suivi le stage,
est la probabilité conditionnelle
![\[P_S(F)=\dfrac{P(S\cap F)}{P(S)}=\dfrac{0,208}{0,25}
=0,832\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/4.png)
- D'après l'arbre, ou la formule des probabilités totales,
on a
![\[P(S)=25\%=52\%\tm40\%+48\%\tm P_{\overline{F}}(S)\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/5.png)
et donc
![\[P_{\overline{F}}(S)=\dfrac{0,25-0.208}{0,48}=\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/6.png)
![\[=\dfrac{P(\overline{F}\cap S)}{P(\overline{F})}
=\dfrac{P(\overline{F}\cap S)}{48\%}=0,0875=8,75\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/7.png)
ce qui est en effet moins de 10% comme l'affirme le directeur.
- D'après l'énoncé, on a
- On note
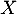 la variable aléatoire qui à un échantillon de
la variable aléatoire qui à un échantillon de  salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
- Pour former un échantillon de 20 salariés, on répète
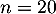 fois
l'expérience aléatoire "désigner au hasard un salarié" dont le succès est
"le salarié a suivi le stage" de probabilité
fois
l'expérience aléatoire "désigner au hasard un salarié" dont le succès est
"le salarié a suivi le stage" de probabilité 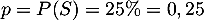 .
Cs répétitions sont supposées identiques et indépendantes car le tirage est assimilé à un tirage avec remise.
.
Cs répétitions sont supposées identiques et indépendantes car le tirage est assimilé à un tirage avec remise.
La variable aléatoire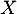 égale au nombre de scuccès, c'est-à-dire au nombre de salarié ayant suivi le stage dans l'échantillon suit donc la loi binomiale de paramètres
égale au nombre de scuccès, c'est-à-dire au nombre de salarié ayant suivi le stage dans l'échantillon suit donc la loi binomiale de paramètres 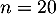 et
et 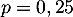 .
.
- À l'aide de la calculatrice, on trouve la probabilité
![\[P(X=5)\simeq 0,202\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/15.png)
- Ce programme calcule les probabilités cumulées, c'est-à-dire
![\[P(X\leqslant k)=P(X=0)+P(X=1)+\dots+P(X=k)\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/16.png)
Lorsque l'on saisit proba(5) dans la console Python, le porgramme retourne donc la valeur
![\[P(X\leqslant5)\simeq0,617\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/17.png)
Il s'agit de la probabilité que moins de 5 personnes aient suivi le stage dans l'échantillon de 20 personnes.
- La probabilité qu'au moins 6 salariés dans un échantillon de 20 aient suivi le stage est
![\[P(X\geqslant6)=1-P(X\leqslant5)\simeq 0,383\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/18.png)
- Pour former un échantillon de 20 salariés, on répète
- 25% des salariés ont suivi le stage et ont donc été augmentés de 5%,
les autres 75% ont été augmentés de 2%.
En moyenne, le pourventage d'augmentation est donc de
![\[25\%\tm5\%+75\%\tm2\%=2,75\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/19.png)
Cacher la correction
Exercice 4: QCM, limite, convexité, primitive
Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n'est demandée.
Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Les six questions sont indépendantes
- La courbe représentative de la fonction
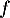 définie sur
définie sur 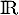 par
par 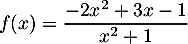 admet pour asymptote
la droite d'équation:
admet pour asymptote
la droite d'équation:
a.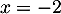
b.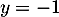
c.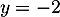
d.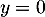
- Soit
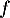 la fonction définie sur
la fonction définie sur 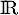 par
par 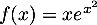 .
.
La primitive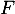 de
de 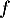 sur
sur 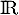 qui vérifie
qui vérifie  est définie par :
est définie par :
a.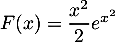
b.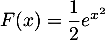
c.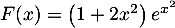 ;
;
d.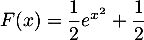
- On donne ci-contre la représentation graphique
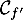 de la fonction dérivée
de la fonction dérivée 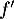 d'une fonction
d'une fonction  définie sur
définie sur  .
.
(10,1)
\psaxes[linewidth=1.25pt,Dx=11,Dy=11](0,0)(-0.5,-5)(10,1)
\psecurve[linewidth=1.25pt,linecolor=blue](-0.3,-6)(-0.2,-5)(0,-4)(1,-1.2)(2,0)(3,0.45)(4,0.5)(5,0.45)(6,0.4)(10,0.1)(11,0.08)
\uput[d](1,0){\footnotesize 1}\uput[d](2,0){\footnotesize 2}\uput[dl](0,0){\footnotesize 0}\uput[d](0,1){\footnotesize 1}
\uput[r](0.4,3.5){$\mathcal{C}_{f'}$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/23.png)
On peut affirmer que la fonction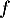 est :
est :
a. concave sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/25.png)
b. convexe sur![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/26.png)
c. convexe sur [0 ; 2]
d. convexe sur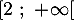
- Parmi les primitives de la fonction
 définie sur
définie sur 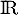 par
par 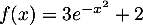 :
:
a. toutes sont croissantes sur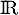
b. toutes sont décroissantes sur
c. certaines sont croissantes sur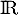 et d'autres
décroissantes sur
et d'autres
décroissantes sur 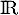
d. toutes sont croissantes sur![$]-\infty~;~0]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/35.png) et
décroissantes sur
et
décroissantes sur 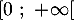
- La limite en
 de la fonction
de la fonction 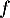 définie sur l'intervalle
définie sur l'intervalle ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022/39.png) par
par 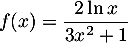 est égale à :
est égale à :
a. ;
;
b.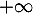 ;
;
c.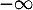
d.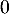
- L'équation
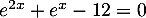 admet dans
admet dans 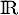 :
:
a. trois solutions;
b. deux solutions;
c. une seule solution;
d. aucune solution.
Correction exercice 4
Cacher la correction
- c.
On a
![\[\begin{array}{ll}f(x) &= \dfrac{-2x^2 + 3x - 1}{x^2 + 1}\\[1em]
&=\dfrac{-2x^2\lp1-\frac3{2x}+\frac1{2x^2}\right)}{x^2\lp1+\frac1{x^2}\right)}\\[1em]
&=-2\dfrac{1-\frac3{2x}+\frac1{2x^2}}{1+\frac1{x^2}}
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/1.png)
d'où
![\[\lim_{x\to+\infty}f(x)=-2\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/2.png)
et donc la droite d'équation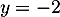 est asymptote.
est asymptote.
- d.
On peut par exemple dériver chacune des propositions, seule la b. et la d. convienne.
Comme on veut de plus que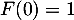 , seule la réponse d. convient finalement.
, seule la réponse d. convient finalement.
- c.
Une fonction est convexe lorsque sa dérivée est croissante (et donc dérivée seconde positive).
Ici on peut conjecturer que la fonction est convexe sur![$]-\infty;3]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/5.png) environ,
et donc en particulier sur
environ,
et donc en particulier sur ![$[0;2]$](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/6.png) .
.
- a.
Les primitives
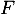 de
de 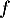 vérifient
vérifient 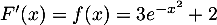 .
En particulier, comme
.
En particulier, comme 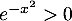 sur
sur 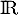 ,
on a
,
on a 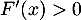 et donc
et donc 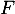 est nécessairement strictement croissante sur
est nécessairement strictement croissante sur 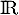 .
.
- d.
On a
![\[f(x) = \dfrac{2\ln x}{3x^2 + 1}
=\dfrac{\ln(x)}{x^2}\tm\dfrac{2}{3+\frac1{x^2}}\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/15.png)
avec, par croissances comparées
![\[\lim_{x\to+\infty}\dfrac{\ln(x)}{x^2}=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/16.png)
et donc
![\[\lim_{x\to+\infty}f(x)=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/17.png)
- c.
On pose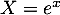 et alors l'équation se réécrit
et alors l'équation se réécrit
![\[X^2+X-12=0\]](/Generateur-Devoirs/TS/ChapIntegration/ex11052022_c/19.png)
c'est une équation du second degré de discriminant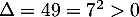 qui admet donc deux solutions réelles distinctes
qui admet donc deux solutions réelles distinctes
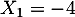 et
et 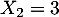 .
.
On revient alors à l'équation de départ:-
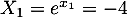 qui est impossible, car
qui est impossible, car 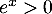 pour tout réel
pour tout réel 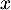
-
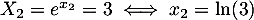
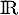 .
.
-
Cacher la correction
Voir aussi: