Longueur d'arc de cercle et aire de secteur
Intersection de secteurs angulaires
Tous les cours et exercices corrigés
{3}
\end{psclip}
\end{pspicture}\]](/Generateur-Devoirs/1S/Chap5/ex13/1.png)
Dans la figure ci-dessus, on a construit un segment
- Quelle est la nature du triangle
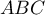 ?
En déduire une mesure de
?
En déduire une mesure de 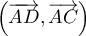 et
et 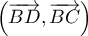
- Quel est le périmètre de la zone hachurée ?
- Quelle est l'aire de la zone hachurée ?
Tous les cours et exercices corrigés